Üçgenin alanını hesaplama formülü: dik, düzenli, ikizkenar, eşkenar

Düzgün, dik ve ikizkenar üçgenin alanını hesaplama formülü nedir ? Bir üçgenin alanını hesaplamanın en kolay ve en sık kullanılan yollarını anlamak için lütfen aşağıdaki makaleye başvurun.

İçindekiler

• 1. Düzenli bir üçgenin alanını hesaplayın
• 2. Bir ikizkenar üçgenin alanını hesaplayın
• 3. Eşkenar üçgenin alanını hesaplayın
• 4. Dik üçgenin alanını hesaplayın
• 5. Dik ikizkenar üçgenin alanını hesaplayın
• 6. Oxyz koordinat sisteminde bir üçgenin alanını hesaplama formülü
• Üçgen çeşitleri

1. Düzenli bir üçgenin alanını hesaplayın

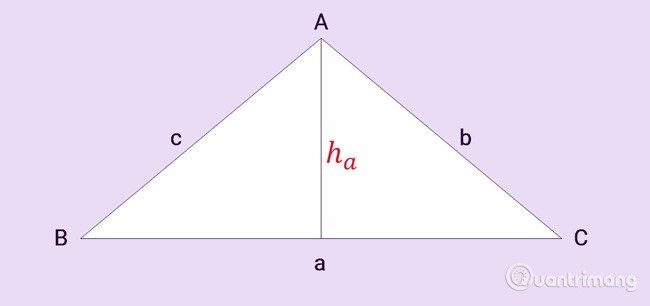
Üçgen ABC'nin üç kenarı vardır a, b, c, ha, A köşesinden yüksekliktir, şekilde gösterildiği gibidir:

A. Genel formül

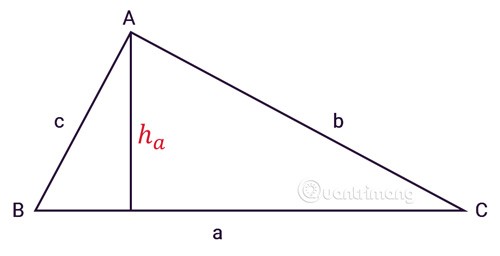
Bir üçgenin alanı, yüksekliğin karşı kenar (taban) uzunluğu ile çarpımı ve 2'ye bölünmesiyle elde edilir.

Düzenli bir üçgenin alanını hesaplamaya ilişkin şiir

Üçgenin alanı kolaydır.
Yüksekliği tabanla çarpıp ikiye bölün.

Örneğin:

Taban uzunluğu 5m, yüksekliği 24dm olan bir üçgenin alanını hesaplayınız.

Çözüm: Yükseklik 24dm = 2,4m

Üçgenin alanı:

B. Bir açısı bilindiğinde bir üçgenin alanını hesaplayın

Bir üçgenin alanı, iki komşu kenarın çarpımının, bu iki kenar arasındaki açının sinüsü ile çarpımının yarısına eşittir.

Örneğin:

ABC üçgeninin kenarı BC = 7, kenarı AB = 5, B açısı ise 60 dereceye eşittir. ABC üçgeninin alanını hesaplayınız?

Ödül:

C. Heron formülünü kullanarak 3 kenarı bilinen bir üçgenin alanını hesaplayın.

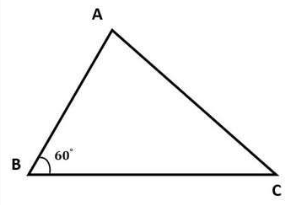
Kanıtlanmış Heron formülünü kullanarak:

Üçgenin yarı çevresi p olmak üzere:

Aşağıdaki formül kullanılarak yeniden yazılabilir:

Örneğin:

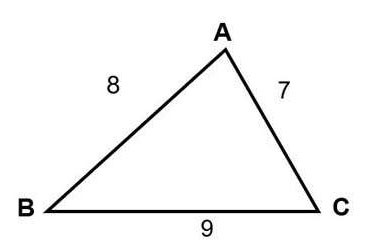
Kenar uzunlukları AB = 8, AC = 7, CB = 9 olan üçgenin alanını hesaplayınız

Ödül:

ABC üçgeninin yarı çevresi

Kahraman formülünü uyguladığımızda

D. Üçgeni (R) çevreleyen dairenin yarıçapını kullanarak alanı hesaplayınız.

Diğer:

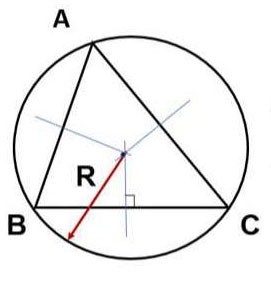
Not: Üçgeni çevreleyen çemberin yarıçapının R olduğunu ispatlamak gerekir.

Örneğin:

ABC üçgeni verildiğinde, kenar uzunlukları a = 6, b = 7, c = 5, R = 3'tür (R, ABC üçgenini çevreleyen çemberin yarıçapıdır). ABC üçgeninin alanını hesaplayınız.

Ödül:

ve. Üçgenin içine çizilen dairenin yarıçapını (r) kullanarak alanını hesaplayınız.

• p: Üçgenin çevresinin yarısı.
• r: İç teğet çemberin yarıçapı.

Örnek: Kenar uzunlukları AB = 20, AC = 21, BC = 15, r = 5 (r, ABC üçgeninin içine çizilen çemberin yarıçapıdır) bilindiğinde ABC üçgeninin alanını hesaplayınız.

Ödül:

Bir üçgenin yarı çevresi:

r= 5

Üçgenin alanı:

2. Bir ikizkenar üçgenin alanını hesaplayın

İkizkenar üçgenler de tıpkı normal üçgenler gibidir, yukarıdaki gibi yüksekliği tabanla çarpıp, 2'ye bölme formülünü uygulayabiliriz. Daha karmaşık ileri formüller de olacak:

İkizkenar üçgen ABC'nin üç kenarı vardır, a taban uzunluğu, b iki kenarın uzunluğu, ha A köşesinden yüksekliktir, şekilde görüldüğü gibi:

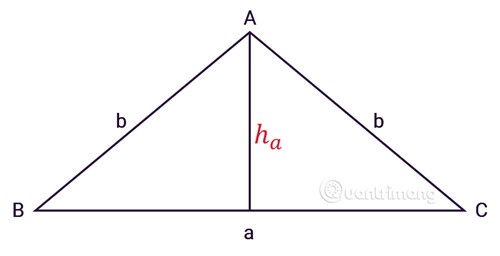
Düzenli üçgenin alan hesaplama formülünü uyguladığımızda, ikizkenar üçgenin alan hesaplama formülünü elde ederiz:

3. Eşkenar üçgenin alanını hesaplayın

Eşkenar üçgen ABC'nin üç eşit kenarı vardır, a kenar uzunluklarıdır, şekilde gösterildiği gibi:

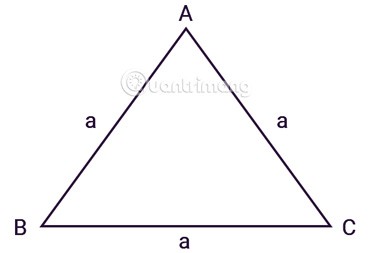
Heron teoremini çıkarıma uygularsak, eşkenar üçgenin alanını hesaplamak için şu formülü elde ederiz:

4. Dik üçgenin alanını hesaplayın

ABC üçgeni B noktasında dik açılıdır, a, b iki dik kenarın uzunluklarıdır:

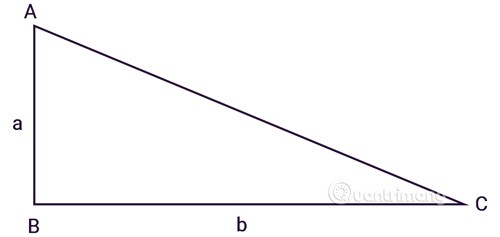
Yüksekliği iki dik kenardan biri, tabanı ise kalan kenar olan bir dik üçgenin alanını hesaplama formülünü uygulayınız.

Dik üçgenin alanını hesaplama formülü:

Dik üçgenin alanını hesaplama ile ilgili şiir:

İki dik açılı üçgen.
Sakin olun, panik yapmayın ve hata yapmayın.

Kenar, kenar çarpılır, ikiye bölünür
alan, egzersizi hızlı yapın

5. Dik ikizkenar üçgenin alanını hesaplayın

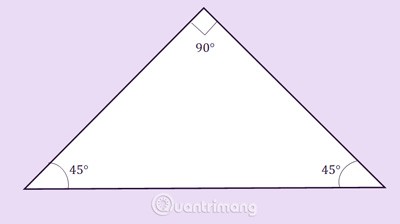
ABC üçgeni A noktasında dik açılı bir üçgendir, a iki kenarın uzunluğudur:

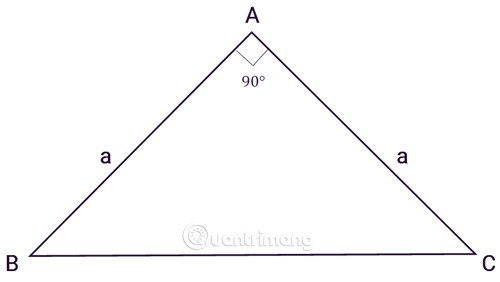
Dik üçgenin alanını hesaplama formülünü, yüksekliği ve tabanı eşit olan ikizkenar dik üçgenin alanına uyguladığımızda formül şu olur:

6. Oxyz koordinat sisteminde bir üçgenin alanını hesaplama formülü

Teorik olarak yukarıdaki formülleri kullanarak uzayda veya Oxyz uzayında bir üçgenin alanını hesaplayabiliriz. Ancak bu durum hesaplamada bazı zorluklara yol açacaktır. Bu nedenle Oxyz uzayında insanlar genellikle bir üçgenin alanını yön çarpımını kullanarak hesaplarlar.

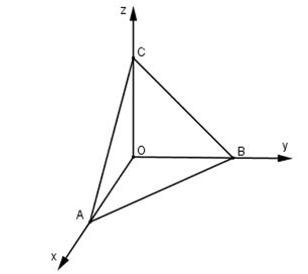
Uzayda Oxyz'de ABC üçgeni verilmiştir. ABC üçgeninin alanı şu formülle hesaplanır:

Örnek :

Oxyz uzayında, A(-1;1;2), B(1;2;3), C(3;-2;0) köşelerinin koordinatlarına sahip ABC üçgeni verilsin. ABC üçgeninin alanını hesaplayınız.

Çözüm :

Sahibiz:

Bir üçgenin alanını hesaplamak için, üçgenin ne tür bir üçgen olduğunu belirlemeniz, oradan doğru alan hesaplama formülünü ve üçgenin alanını hesaplamak için gerekli faktörleri olabildiğince çabuk bulmanız gerekir.

Üçgen çeşitleri

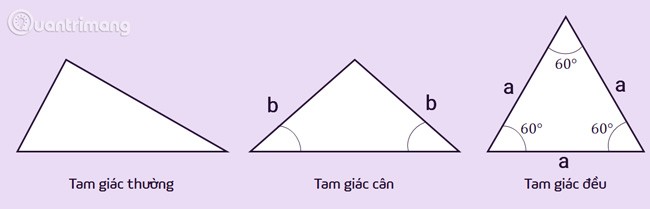
Düzgün üçgen: En temel üçgendir, farklı kenar uzunluklarına, farklı iç açı ölçülerine sahiptir. Düzgün üçgenler aynı zamanda üçgenlerin özel durumlarını da içerebilir.

İkizkenar üçgen: İki kenarı eşit olan üçgendir, bu iki kenara iki yanal kenar denir. İkizkenar üçgenin tepe noktası, iki komşu kenarın kesişim noktasıdır. Tepe noktasının oluşturduğu açıya tepe açısı, diğer iki açıya ise taban açıları denir. İkizkenar üçgenin özelliği tabandaki iki açının birbirine eşit olmasıdır.

Eşkenar üçgen: Üç kenarı da eşit olan ikizkenar üçgenin özel bir halidir. Eşkenar üçgenin özelliği 3 eşit açısının olması ve 60 derece olmasıdır.

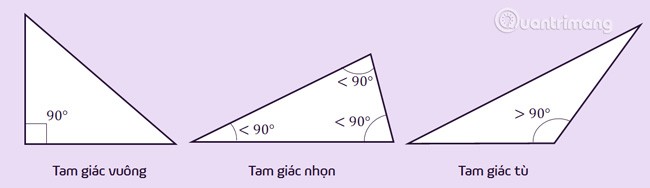
Dik üçgen: Bir açısı 90 derece olan üçgendir (dik açı).

Geniş açılı üçgen: İç açısı 90 dereceden büyük (geniş açı) veya dış açısı 90 dereceden küçük (dar açı) olan üçgendir.

Dar üçgen: Üç iç açısının hepsi 90 dereceden küçük (üç dar açı) veya tüm dış açılarının hepsi 90 dereceden büyük (altı geniş açı) olan üçgendir.

Dik ikizkenar üçgen: Hem dik üçgen hem de ikizkenar üçgendir.

• Bir üçgenin çevresini hesaplama formülü
• Düzenli, ikizkenar, eşkenar ve dik üçgenlerde yüksekliği hesaplama formülü
• Odak noktası nedir? Bir üçgenin ağırlık merkezini hesaplama formülü
• Dik açıortay nedir?

Yukarıda, oxyz koordinat sisteminde üçgen alanının hesaplanmasına ilişkin yaygın üçgen alanı hesaplama formüllerinin bir özeti verilmiştir. Herhangi bir endişeniz, sorunuz veya katkınız varsa lütfen Quantrimang.com ile görüşmek üzere aşağıya bir yorum bırakın.