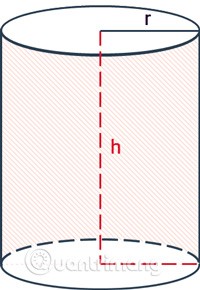
Derste ve günlük hayatımızda kullanabileceğimiz silindirin yanal alanı, toplam alanı ve yüksekliğinin hesaplanması formülünü öğrenelim.
İçindekiler
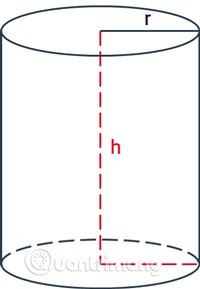
Bir silindirin alanı nasıl hesaplanır
Silindirin alanı yanal alanı ve toplam alanı içerir.
Aşağıdaki tabloya silindirin yüksekliğini ve yarıçapını girerek silindirin yanal alanını ve toplam alanını öğrenebilirsiniz.
Bir silindirin yanal alanını hesaplama formülü
Bir silindirin yanal alanı, sadece silindiri çevreleyen yüzeyin alanını içerir, iki tabanın alanını içermez.
Bir silindirin yanal alanını hesaplama formülü, taban çemberinin çevresinin yükseklikle çarpılmasıyla bulunur.
 |
Orada:
- Çevre, çevreleyen alandır.
rsilindirin yarıçapıdır.hyükseklik, silindirin iki tabanı arasındaki mesafedir.
|
Örnek: 1
Taban yarıçapı r = 5 cm, yüksekliği h = 7 cm olan dairesel silindir. Düşey silindirin yanal alanını hesaplayınız.
Çözüm: Dairesel silindirin yüzey alanı: Sxq = 2.π.rh = 2π.5.7 = 70π = 219,8 (cm2).
Örnek: 2
Kenar uzunluğu 2a olan ABCD karesi verilsin. AB ve CD kenarlarının orta noktaları sırasıyla O ve O' olsun. Bu kareyi OO' ekseni etrafında döndürdüğümüzde dönen bir silindir elde ederiz. Dönen silindirin yüzey alanını hesaplayınız.
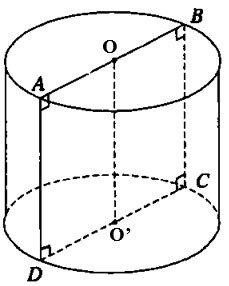
Çözüm:
Taban çemberinin yarıçapı r=CD=a
Silindirin yüksekliği h= OO'= AD=2a
Yani silindirin yan alanı Sxq = 2πrh = 2π.a.2a =4a2π
Bir silindirin toplam alanını hesaplama formülü
Toplam alan, şeklin kapladığı tüm alanın, yanal alan ve iki dairesel taban alanı da dahil olmak üzere büyüklüğü olarak hesaplanır.
Bir silindirin toplam alanını hesaplama formülü, yanal alan artı iki taban alanıdır.
Örnek 1 : Tabanı 3, yüksekliği 5 olan bir silindirin toplam alanını hesaplayınız.
Çözüm:
Toplam alan Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Silindirin yüksekliğini hesaplayın
Bir silindirin yüksekliği, silindirin iki tabanı arasındaki mesafedir.
Toplam alanı ve taban yarıçapını bildiğinizde bir silindirin yüksekliğini hesaplayın
Örnek: Taban yarıçapı R = 8cm ve toplam alanı 564π cm2 olan bir silindir verilmiştir. Silindirin yüksekliğini hesaplayınız.
Ödül:
Sahibiz
Yanal alanı bildiğinizde bir silindirin yüksekliğini hesaplayın
=>
Bir silindirin taban yarıçapını hesaplama formülü
1. Bir dairenin çevresini hesaplama formülü; daire alanı
Çemberin çevresi C=2πr'dir
=>
Tabanı olan dairenin alanı S=πr2'dir
=>
Örneğin. Aşağıdaki durumlarda silindir tabanının yarıçapını hesaplayınız:
A. Taban çemberinin çevresi 6π'dir
B. Taban alanı 25π'dir
Çözüm:
A. Taban çemberinin yarıçapı
B. Taban çemberinin yarıçapı
2. Taban, çokgenin içine çizilen dairedir.
- Herhangi bir üçgene yazılır: S üçgenin alanı ve p yarı çevredir
- Eşkenar bir üçgenin içine yazılmış: kenar
- Yazılı kare:
Örnek 1 . Kenarı a olan bir küpün içine çizilmiş bir silindir verilmiştir. Bu silindirin yarıçapını hesaplayın.
Silindirin yarıçapı:
Örnek 2 . ABC.A'B'C' düzgün prizması verildiğinde, silindirin etrafındaki hacim belirlenir. Bu silindirin yarıçapını hesaplayın.
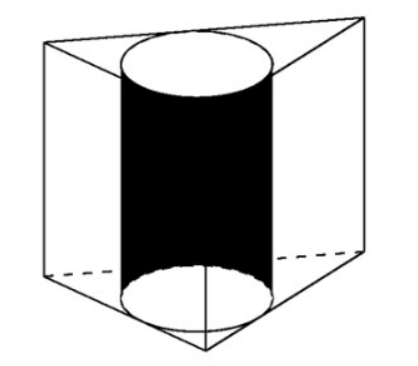
Prizmanın hacmi
Düzenli bir prizmanın tabanı eşkenar üçgendir, bu nedenle => kenar
Dolayısıyla silindir tabanının yarıçapı:
3. Taban, çokgeni çevreleyen dairedir.
Herhangi bir üçgenle çevrelenmiş:
Orada:
- a, b, c üçgenin üç kenarının uzunluklarıdır
- p üçgenin yarı çevresidir:
Dik üçgenin çevresi: hipotenüs
Eşkenar üçgenin çevresi: kenar
Karenin çevresi: kenar
Örneğin:
Aşağıdaki durumlarda S.ABC düzgün piramidini çevreleyen silindirin taban yarıçapını hesaplayınız:
A. ABC, AB = a ve AC = a√3 olan A noktasında bir dik üçgendir
B. ABC'nin AB= 5 olduğu; AC= 7; MÖ=8
Ödül:
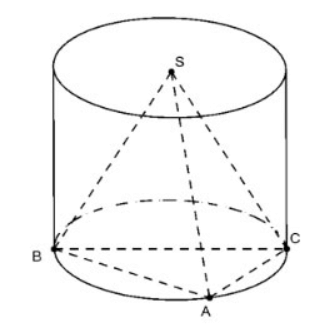
A. Hipotenüs
Çünkü ABC, A noktasında dik açıdır, yarıçap R=0.5.BC=a
B. ABC üçgeninin yarı çevresi
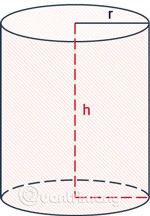
Dairesel silindir nedir?
Dairesel silindir, birbirine paralel iki eşit dairesel tabana sahip silindirdir.
Basitten karmaşığa doğru geometri problemlerinde silindirler sıklıkla kullanılır ve silindirlerin alan ve hacim hesaplama formülleri çoğu zaman farklı kullanılır. Bir dairenin alanını ve çevresini nasıl hesaplayacağınızı biliyorsanız, bir silindirin hacmini, yanal alanını ve toplam alanını hesaplama formüllerini kolayca çıkarabilirsiniz.
Bir silindirin kesit alanının hesaplanması için formül
Silindiri eksenden geçen düzlem (P) ile kesin
- Ortaya çıkan kesit bir dikdörtgendir.
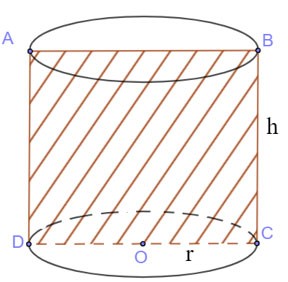 |
Kesit alanı:
SABCD = BC.CD =2r.h
|
Silindiri eksene paralel ve eksenden x uzaklıkta bir düzlem (P) ile kesin.
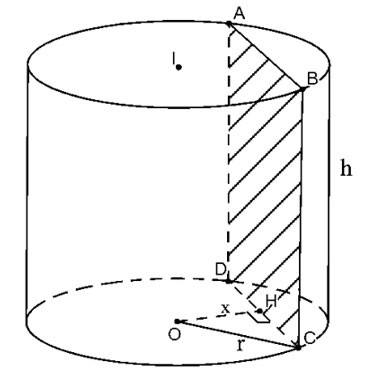 |
Elde edilen kesit yukarıda gösterildiği gibi ABCD dikdörtgenidir.
H, CD'nin orta noktası olsun, OH ⊥ CD=>
Bu nedenle kesit alanı
|
Silindiri eksene dik olmayan bir düzlem (P) ile kesin ancak silindirin tüm jeneratörlerini kesin
 |
Oluşan kesit, merkezi O' ve yarıçapı O'A'=r olan bir dairedir.
Kesit alanı: S= πr2
|
Silindiri eksene dik olmayan düzlem (P) ile kesin ancak silindirin tüm üreteçlerini kesin.
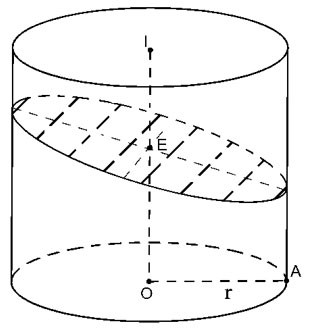 |
Ortaya çıkan kesit, küçük ekseni 2r => a=r olan bir Elips (E)'dir.
Büyük eksen eşittir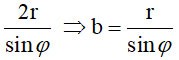
 OI ekseni ile (P) arasındaki açıdır OI ekseni ile (P) arasındaki açıdır
Bu nedenle alan S = π'dir. ab=
|
Bir silindirin alanının hesaplanmasına örnek
Ders 1 :
Bir silindirin yanal alanı 13 cm taban çevresi ve 3 cm yüksekliği olan dairesel bir şekle sahiptir.
Ödül:
Şunlara sahibiz: Çemberin çevresi C = 2R.π = 13cm, h = 3cm
Yani silindirin yanal alanı:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Ders 2 : Taban dairesinin yarıçapı 6 cm olan bir silindir verilmiştir. Silindirin tabanından tepesine kadar olan yüksekliği ise 8 cm'dir. Silindirin yanal alanı ve toplam alanı kaçtır?
Ödül
Formüle göre taban yarım dairesi r = 6 cm, silindirin yüksekliği h = 8 cm'dir. Dolayısıyla bir silindirin yanal alanını ve toplam alanını hesaplamak için formülümüz şu şekildedir:
Silindirin yüzey alanı = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Silindirin toplam alanı = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Ders 3 : Taban yarıçapı 7 cm olan bir silindirin yanal alanı 352 cm2'dir.
O zaman silindirin yüksekliği:
(A) 3,2 cm; (B) 4,6 cm; (C) 1,8 cm
(D) 2,1 cm; (E) Başka bir sonuç
Lütfen doğru sonucu seçin.
Çözüm: Bizde var
Yani cevap E'dir.
Ders 4 : Bir silindirin yüksekliği taban çemberinin yarıçapına eşittir. Silindirin yanal alanı 314 cm2'dir. Taban çemberinin yarıçapını ve silindirin hacmini hesaplayın (sonucu iki ondalık basamağa yuvarlayın).
Ödül:
Silindirin yanal alanı 314cm2'dir
Sxq = 2.π.rh = 314'tür
Burada r = h
Yani 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Silindirin hacmi: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Umarım yukarıdaki makale silindirler hakkında temel ve ileri düzeydeki bilgileri, bir silindirin toplam alanını ve yanal alanını nasıl hesaplayacağınızı kavramanıza yardımcı olmuştur.










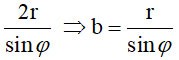
 OI ekseni ile (P) arasındaki açıdır
OI ekseni ile (P) arasındaki açıdır











