Rasyonel sayı nedir? İrrasyonel sayı nedir?

Rasyonel ve irrasyonel sayıların tanımları ve formülleri, öğrencilerin sağlam bir matematiksel temele sahip olmaları için anlamaları gereken önemli bir matematik bilgisidir. Aşağıdaki makalede sizlere rasyonel ve irrasyonel sayıların tanımı, özellikleri ve matematiksel formları tanıtılmaktadır. Lütfen ona bakınız.

Rasyonel sayılar, irrasyonel sayılar

• Rasyonel sayı nedir?
  • Rasyonel sayıların sınıflandırılması
  • Rasyonel sayıları sayı doğrusunda gösterme
  • Rasyonel sayıları toplayın ve çıkarın
  • Rasyonel sayıları çarpma ve bölme
  • Bir rasyonel sayının mutlak değeri
  • İki rasyonel sayıyı karşılaştırın
  • Rasyonel bir sayının kuvvetini hesaplama formülü
• İrrasyonel sayı nedir?
  • İrrasyonel sayı kavramı
  • İrrasyonel sayıların özellikleri
• Rasyonel ve irrasyonel sayılar arasındaki fark nedir?
• Sayı kümelerinin ilişkisi
• Rasyonel sayılarla ilgili alıştırmalar

Rasyonel sayı nedir?

- Rasyonel sayılar, kesir (bölüm) şeklinde yazılabilen sayılar kümesidir. Yani bir rasyonel sayı sonsuz sayıda tekrarlayan ondalık sayı ile gösterilebilir.

- Rasyonel sayılar şeklinde yazılır. Burada a ve b birer tam sayıdır ancak b 0'dan farklı olmalıdır.

- Rasyonel sayılar kümesidir.

=> Rasyonel sayılar kümesi: .

Örneğin: , , … rasyonel sayılardır.

• Herhangi bir a tam sayısı rasyonel sayıdır çünkü a tam sayısı biçiminde yazılabilir.

Örneğin: Rasyonel sayılar var.

Sahibiz:

Yorum: hepsi rasyonel sayılardır.

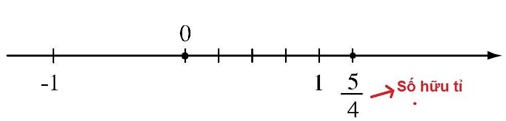
Rasyonel sayıların sınıflandırılması

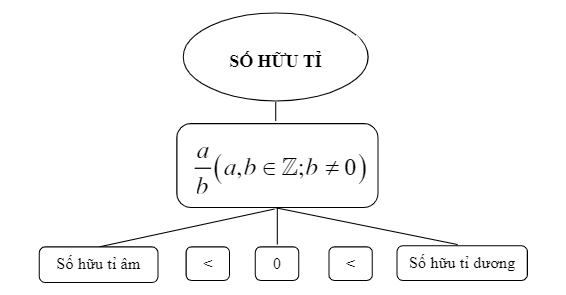
Rasyonel sayılar ikiye ayrılır: Negatif rasyonel sayılar ve pozitif rasyonel sayılar. Özellikle:

• Negatif rasyonel sayılar: 0'dan küçük rasyonel sayıları içerir.
• Pozitif rasyonel sayılar: 0'dan büyük rasyonel sayıları içerir.

Not: 0 sayısı ne negatif ne de pozitif bir rasyonel sayıdır.

Doğa

• Rasyonel sayılar kümesi sayılabilir bir kümedir.
• Değişmeli özellik:
• 0 ile toplama özelliği:
• Kombine özellikler:

Rasyonel sayıları sayı doğrusunda gösterme

- Rasyonel sayıları sayı doğrusunda göstermek için şu çarpanları kullanırız:

Adım 1: Rasyonel sayıyı kesir olarak yazın

Adım 2: Birim doğru parçasını b eşit parçaya bölerek eski birimin yeni bir birim parçasını elde edin.

Adım 3: Rasyonel sayı, A noktasının 0 noktasından yeni bir birim uzaklıkta olmasıyla gösterilir.

• A negatif bir sayı ise 0'ın solundadır.
• A, pozitif bir sayı ise 0'ın sağındadır.

Örneğin: Şekilde P noktası rasyonel sayıyı temsil etmektedir:

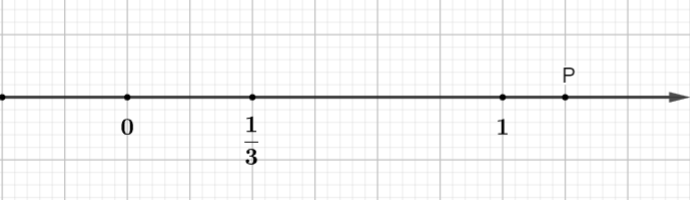
Talimat vermek

Birim doğru parçası 6 eşit parçaya bölünmüştür (yeni birim eski birimin 1/6'sıdır)

P noktası, O noktasından 7 yeni birim uzaklıkta bulunmaktadır.

Ve P noktası O noktasının sağındadır, dolayısıyla P pozitif bir rasyonel sayıdır.

Yani P bir rasyonel sayıyı temsil eder.

Rasyonel sayıları toplayın ve çıkarın

i) İki rasyonel sayıyı toplama ve çıkarma kuralları

x ve y rasyonel sayılarını iki kesir olarak yazıp, kesirleri toplama ve çıkarma kurallarını uygulayarak toplayabilir ve çıkarabiliriz.

Bizde:

ii) Özellikler

- Rasyonel sayılarda toplama işlemi kesirlerin toplanmasına benzer özellikler taşır: Değişmeli, birleşmeli, 0 ile toplama, zıt yönlü toplama.

- Sahibiz:

a) Değişmeli özellik:

b) İlişkisel özellikler:

c) 0 ekleyin:

d) Karşı sayıyı ekle:

iii, Geçiş kuralları

Bir terimi denklemin bir tarafından diğer tarafına taşırken o terimin işaretini değiştirmemiz gerekir.

Q'da, terimleri yer değiştirebileceğimiz, tam sayılar kümesindeki cebirsel toplamlar gibi terimleri keyfi olarak gruplamak için parantez koyabileceğimiz bir cebirsel toplamımız var.

• Eğer öyleyse
• Bizde:

Rasyonel sayıları çarpma ve bölme

i) İki rasyonel sayıyı çarpma ve bölme kuralları

- İki rasyonel sayıyı kesir olarak yazıp, kesirlerde çarpma ve bölme kurallarını uygulayarak çarpabilir ve bölebiliriz.

• Bizde:
• Bizde:

Örneğin:

Rasyonel sayıları çarpma: 

Rasyonel sayıları bölme: 

ii) Özellikler

- Rasyonel sayılarla çarpma işlemi de kesirlerle çarpma işleminin aynı özelliklerine sahiptir: Değişmeli, birleşmeli, 1 ile çarpma ve toplama işleminde çarpmanın dağılma özelliği.

- Sıfırdan farklı her rasyonel sayının bir tersi vardır.

- Sahibiz:

• Değişmeli özellik: .
• İlişkisel özellikler: .
• 1 ile çarpmanın özelliği: .
• Dağıtım özellikleri: .
• İle . a'nın karşılıklısı 'dir.

Bir rasyonel sayının mutlak değeri

- Bir rasyonel sayı olan a'nın mutlak değeri, ile gösterilir ve sayı doğrusu üzerinde a noktasından 0 noktasına olan uzaklığa eşittir.

Örneğin:

(Çünkü )

(Çünkü )

İki rasyonel sayıyı karşılaştırın

- Herhangi 2 rasyonel sayı için her zaman ya da ya da olur.

- İki rasyonel sayıyı karşılaştırmak için aşağıdakileri yaparız:

• Aynı pozitif paydaya sahip 2 kesri şöyle yazalım:
• Paydaları a, b tam sayıları olarak karşılaştırın:

Örneğin: İki rasyonel sayıyı karşılaştırın: ve

Sahibiz:

Çünkü iyidir.

Rasyonel bir sayının kuvvetini hesaplama formülü

Rasyonel sayıların kuvvetlerini hesaplamak için hatırlamanız gereken formüller

• Aynı tabana sahip iki kuvvetin çarpımı:
• Gücün gücü
• Bir ürünün gücü
• Bölümün kuvveti

İrrasyonel sayı nedir?

İrrasyonel sayı kavramı

• Rasyonel sayılardan bahsedildiğinde akla irrasyonel sayılar gelmeden olmaz. Bunlar sonsuz, tekrarlanmayan ondalık sayılar şeklinde yazılan ve ile gösterilen sayılardır.
• Rasyonel sayı olmayan gerçek sayılar oran olarak gösterilemez.

Örneğin: 3.145248… irrasyonel bir sayıdır.

İrrasyonel sayıların özellikleri

İrrasyonel sayılar kümesi sayılamaz bir kümedir.

Örneğin:

İrrasyonel sayılar: 0.1010010001000010000010000001… (bu sonsuz tekrar etmeyen bir ondalık sayıdır)

Karekök sayısı: √2 ​​(karekök)

Pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Rasyonel ve irrasyonel sayılar arasındaki fark nedir?

• Rasyonel sayılar, sonlanmayan tekrar eden ondalık sayıları içerirken, irrasyonel sayılar, sonlanmayan tekrar etmeyen ondalık sayıları içerir.
• Rasyonel sayılar sadece kesirlerden oluşurken, irrasyonel sayılar birçok farklı sayı türüne sahiptir.
• Rasyonel sayılar sayılabilir sayılardır, irrasyonel sayılar ise sayılamaz sayılardır.

Sayı kümelerinin ilişkisi

Sayı kümelerinin sembolleri:

• N: Doğal sayılar kümesi
• N*: 0 dışındaki doğal sayılar kümesi
• Z: Tam sayılar kümesi
• S: Rasyonel sayılar kümesi
• I: İrrasyonel sayılar kümesi

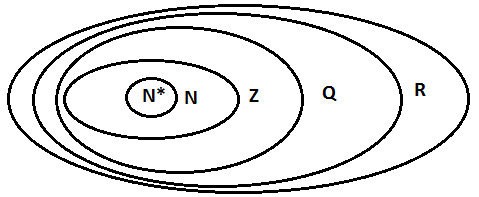
Şunu elde ederiz: R = Q ∪ I.

N'yi ayarla; Z ; Q; R.

Daha sonra sayı kümeleri arasındaki dahil etme ilişkisi şu şekildedir: N ⊂ Z ⊂ Q ⊂ R

Rasyonel sayılarla ilgili alıştırmalar

Form 1: Rasyonel sayılarla ilgili hesaplamalar yapın

Çözüm yöntemi: Rasyonel sayılarla ilgili işlemleri yapmaya yönelik alıştırmaları çözmek için önce rasyonel sayıları kesre dönüştürün, ardından rasyonel sayılarda toplama, çıkarma, çarpma ve bölme işlemlerini yaparken işlem kurallarını uygulayın.

Örnek: Hesapla  

Cevap:

Form 2: Rasyonel sayıları sayı doğrusunda gösterme

Çözüm: Rasyonel sayının pozitif rasyonel sayı mı yoksa negatif rasyonel sayı mı olduğunu belirlemeniz ve ardından bir sonraki adımlara geçmeniz gerekir:

• Rasyonel sayı a/b pozitif bir rasyonel sayı ise: Sayı doğrusunda pozitif yönde, 1 birimlik uzunluğu b eşit parçaya böleriz. Daha sonra Öküz ekseninin pozitif yönünde bir nokta alıp, bir parçayı işaret ederek a/b rasyonel sayısının konumunu belirleyiniz.
• Rasyonel sayı a/b negatif bir rasyonel sayı ise: Sayı doğrusu üzerinde eksenin negatif yönünde, 1 birim uzunluğunu b eşit parçaya böleriz. Daha sonra Öküz ekseninin negatif yönünde bir nokta alıp, bir parçayı işaret ederek a/b rasyonel sayısının konumunu belirleyiniz.

Form 3: Rasyonel sayıları karşılaştırma

Çözüm: Verilen rasyonel sayıları aynı pozitif paydaya sahip kesirlere dönüştürün, ardından paylarını karşılaştırın. Cevabı bulmak için daha ileri seviyedeki kesirlerle karşılaştırma yapabiliriz.

Form 4: Bir rasyonel sayının negatif, pozitif veya 0 olup olmadığını belirleyin

Çözüm yöntemi: 4. tip alıştırmaları çözmek için öğrencilerin rasyonel sayıların özelliklerini temel alarak rasyonel sayının negatif, pozitif veya 0 olduğunu belirlemeleri gerekir.

Örneğin: Rasyonel sayı x = (a – 25)/29 verildiğinde, a'nın değerini şu şekilde belirleyin:

• x negatiftir
• x pozitiftir
• x = 0

Cevap:

x negatif bir sayıdır => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x pozitif bir sayıdır => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Form 5: Verilen koşullara göre aralıktaki rasyonel sayıları bulun

Çözüm: Eğer soruda verilen koşullara göre bir aralıktaki rasyonel sayıların bulunması isteniyorsa, cevabı bulmak için rasyonel sayıları aynı paya veya paydaya koymamız gerekir.

Örnek: m'nin büyük ve küçük değerlerini bulun

Cevap kılavuzu

Kesirleri ortak paydalara şu şekilde dönüştürün:

Ortak payda: 18

Sorumuza göre;

Form 6: Rasyonel sayılarla x'i bulun

Matematik problemlerini çözme yöntemi: Matematik problemlerinde rasyonel sayılarla x'i bulmak için ortak payda indirgemesi yapmak ve x'i bir tarafa, kalan terimleri de 1'e dönüştürmek gerekir. Buradan x değerini hesaplayın

Örnek: x'i bilerek x'i bul. (2/ 3) + 5/ 6 = 1/ 8

Cevap:

X . (2/ 3) + 5/ 6 = 1/ 8

=> x. (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Form 7: İfadenin tam sayı olmasını sağlayacak şekilde bir değer bulun

Matematik problemlerini çözme yöntemi: a'yı bulma probleminde, eğer payda a yoksa bölünebilme işaretini kullanmamız gerekir. Payda a varsa, bölünebilme işaretini kullanın veya payı paydaya ayırın. Eğer problem hem a hem de b'yi aynı anda bulmayı gerektiriyorsa, a veya b'yi gruplandırıp hesaplama için kesirli forma dönüştürün.

Örnek: 8/(a – 1)'in tam sayı olması koşuluyla tam sayı a'yı bulun

Cevap:

Koşul: a – 1 ≠ 0 => a ≠ 1

a bir tam sayı olsun => 8 (a – 1)'e bölünebilir

=> (a – 1) 8'in bir faktörüdür => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Umarım yukarıdaki makale rasyonel sayıların ne olduğunu, irrasyonel sayıların ne olduğunu, rasyonel sayı türlerinin ne olduğunu, rasyonel sayı sembollerinin ne olduğunu ve rasyonel sayıların nasıl tanınarak problemleri kolayca çözebileceğinizi anlamanıza yardımcı olmuştur.

Yukarıda verilen irrasyonel sayılar ve rasyonel sayılar hakkındaki bilgilere ek olarak, kesirler , karma sayılar , ondalık sayılar gibi diğer bazı matematik bilgilerine de başvurabilirsiniz .