Paralelkenarın alan ve çevresini hesaplama formülü temel bilgidir. Lütfen aşağıda Quantrimang.com'un derlediği formüle bakınız.
İçindekiler
1. Paralelkenarın alanı
Bir paralelkenarın alanı, paralelkenarın gözle görülebilen düz kısmı olan yüzey alanının büyüklüğü ile ölçülür.
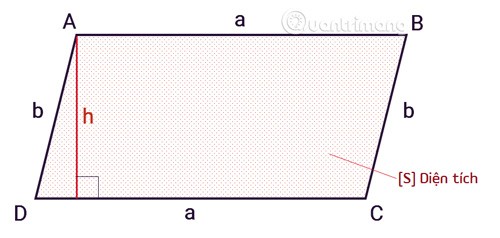
Paralelkenarın alanı , taban ile yüksekliğin çarpımına eşit olan formülle hesaplanır .
SABCD = axh
Orada:
Sbir paralelkenarın alanıdır.aparalelkenarın tabanıdır.hBir paralelkenarın tepesinden tabanına kadar olan yüksekliktir.
2. Paralelkenarın çevresi
Bir paralelkenarın çevresi, şekli çevreleyen doğruların uzunlukları, yani tüm alanı çevreleyen doğruların uzunlukları eklenerek hesaplanır ve bu, herhangi bir çift komşu kenarın toplamının 2 katına eşittir.
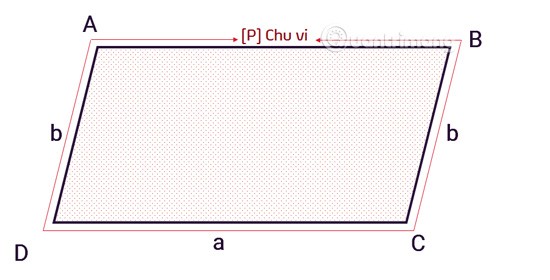
Başka bir deyişle, paralelkenarın çevresi dört kenarının uzunluklarının toplamına eşittir. Spesifik formül şu şekildedir:
C = 2x (a+b)
Orada:
Cbir paralelkenarın çevresidir.ave bbir paralelkenarın bitişik kenarlarıdır.
3. Paralelkenar nedir?
Tanımlamak
Paralelkenar, 2 çift paralel kenarı veya 1 çift paralel ve eşit kenarı olan dörtgendir. Paralelkenar, şeklin orta noktasında kesişen iki eşit karşılıklı açıya ve iki köşegene sahiptir.
Paralelkenar, yamukların özel bir hali olarak düşünülebilir.
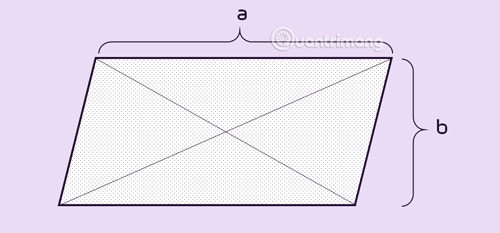
Paralelkenarın özellikleri
Paralelkenarda:
- Karşılıklı kenarları eşittir.
- Karşılıklı açılar eşittir.
- Her doğrunun orta noktasında iki köşegen kesişir.
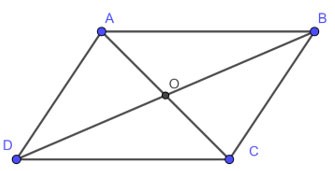
ABCD bir paralelkenardır, AC, BD'yi O noktasında keser. O zaman:
• AB = CD, AD = BC
•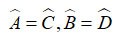
• OA = OC, OB = OD
Tanınmanın belirtileri
a) Karşılıklı kenarları paralel olan dörtgene paralelkenar denir.
b) Karşılıklı kenarları eşit olan dörtgene paralelkenar denir.
c) Karşılıklı iki kenarı paralel ve eşit olan dörtgene paralelkenar denir.
d) Karşılıklı açıları birbirine eşit olan dörtgene paralelkenar denir.
e) Köşegenleri orta noktada kesişen iki köşegenden oluşan dörtgene paralelkenar denir.
4. Paralelkenarları gözden geçirmek için çoktan seçmeli sorular
Alıştırma 1 : Yanlış cümleyi seçin.
A. Bir paralelkenarın, her bir köşegenin orta noktasında kesişen iki köşegeni vardır.
B. Paralelkenarın iki eşit zıt açısı vardır
C. Paralelkenarın birbirine dik iki köşegeni vardır.
D. İki paralelkenarın iki çift paralel, karşılıklı kenarı vardır.
Çözüm
Paralelkenarda:
+ Paralelkenarın zıt kenarları paraleldir
+ Karşı taraflar eşittir
+ Her doğrunun orta noktasında iki köşegen kesişiyor bu yüzden C yanlıştır.
Doğru cevap: C
Alıştırma 2 : Â = α > 900 olan ABCD paralelkenarı verilmiştir. Paralelkenarın dışına ADE, ABF eşkenar üçgenlerini çizin. CEF üçgeni nasıl bir üçgendir? En iyi cevabı seçin
A. Üçgen
B. İkizkenar üçgen
C. Eşkenar üçgen
D. Geniş açılı üçgen
Cevap:
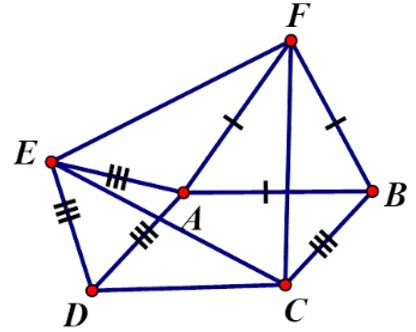

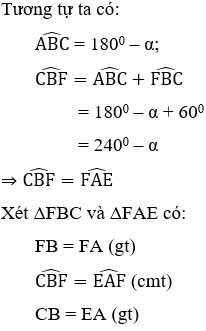
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
(1) ve (2)'den CF = FE = EC olduğunu çıkarabiliriz, dolayısıyla CEF üçgeni eşkenardır.
Ders 3 : Yanlış cümleyi seçin. ABCD bir paralelkenardır. Daha sonra:
A.AB = CD
B. AD = M.Ö.
C. Cevaplı paralelkenar testi
D. AC = BD
Çözüm
Paralelkenarda:
+ Paralelkenarın zıt kenarları paraleldir
+ Karşı taraflar eşittir
+ Her doğrunun orta noktasında iki köşegen kesişiyor bu yüzden D yanlıştır.
Ders 4 : Boşluğu uygun ifadeyle doldurun: "İki köşegeni olan bir dörtgen... bir paralelkenardır."
A. eşit
B. kesişmek
C. her çizginin orta noktasında kesişir
D. paralel
Çözüm
İşaretler:
Köşegenleri orta noktada kesişen iki köşegenden oluşan dörtgene paralelkenar denir.
Ders 5 : Yanlış cümleyi seçin:
A. Karşılıklı iki çift paralel kenarı olan dörtgene paralelkenar denir.
B. Tabanına bitişik iki eşit açısı bulunan yamuğa paralelkenar denir.
C. Karşılıklı iki eşit kenarı bulunan dörtgene paralelkenar denir.
D. İki çift eşit zıt açıya sahip olan dörtgene paralelkenar denir.
Çözüm
İşaretler:
+ Karşılıklı kenarları paralel olan bir dörtgen paralelkenardır, dolayısıyla A doğrudur.
+ Karşılıklı kenarları eşit olan bir dörtgen paralelkenardır, dolayısıyla D doğrudur.
+ Karşılıklı açıları birbirine eşit olan dörtgene paralelkenar denir dolayısıyla D doğrudur.
Tabanına bitişik iki eşit açısı olan yamukların ikizkenar yamuk olduğu bilindiğinden B yanlıştır.
Doğru cevap: B
5. Paralelkenarın çevresini ve alanını hesaplama örnekleri
Örnek 1 : Tabanı 12 cm, kenarı 7 cm ve yüksekliği 5 cm olan bir paralelkenar verilmiştir. Bu paralelkenarın çevresini ve alanını hesaplayınız?
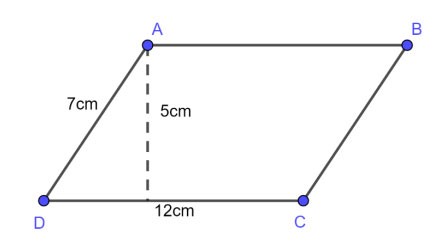
Ödül:
Paralelkenarın çevresi:
Ç = 2 x (12 + 7) = 38 (cm)
Bir paralelkenarın alanı:
S = axh = 12 x 5 = 60 (cm2)
Örnek 2:
H ve K'nin sırasıyla A, C ve BD köşelerinden çizilen yüksekliklerin ayakları olduğu ABCD paralelkenarı verilmiştir.
a) AHCK'nın bir paralelkenar olduğunu gösteriniz.
b) HK'nin orta noktası O olsun. A, O, C'nin aynı doğru üzerinde olduğunu gösteriniz.
Talimat:
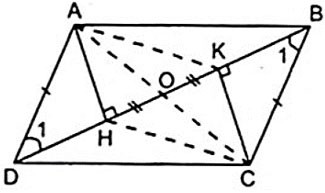
a) Hipotezden şunu elde ederiz:
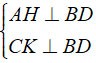 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
Paralelkenarın kenarlarının özelliklerini ve alternatif açıların özelliklerini uygulayarak şunu elde ederiz:
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(hipotenüs – dar açı durumu)
⇒ AH = CK (karşılık gelen kenarlar eşittir) ( 2 )
(1) ve (2)'den, karşı kenarları paralel ve eşit olan AHCK dörtgenini elde ederiz; bu bir paralelkenardır.
b) AHCK paralelkenarının köşegenlerinin özelliklerini uygulayın
AHCK paralelkenarının her bir doğrunun orta noktasında kesişen AC ve HK adlı iki köşegeni vardır. Çünkü O, HK'nin orta noktası olduğundan, O aynı zamanda AC'nin de orta noktasıdır.
⇒ A, O, C doğru bir doğru üzerindedir.
Paralelkenarların yanı sıra eşkenar dörtgen , kare , yamuk , dikdörtgen gibi diğer yaygın geometrik şekillerin alan ve çevre hesaplama formülleri de çok önemlidir ve çalışma ve yaşamda yaygın olarak uygulanır.
Umarım yukarıdaki makale sayesinde paralelkenarlar hakkında temel bilgileri daha iyi anlamış ve kavramışsınızdır. Quantrimang.com ile görüşmek istediğiniz herhangi bir soru veya yorumunuz varsa lütfen aşağıya yorum bırakın.




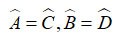



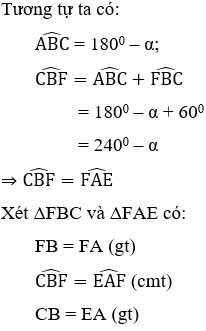


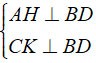 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK










