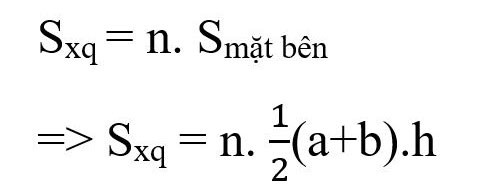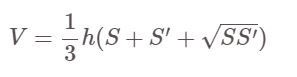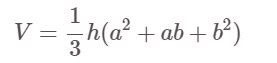Kesik piramidin hacmini, yanal alanını ve kesik piramidin toplam alanını hesaplama formülü

Kesik piramit nedir, kesik piramidin hacmi nasıl hesaplanır, kesik piramidin yan alanı ve toplam alanı nasıl hesaplanır gibi konuları aşağıdaki yazımızda öğrenelim.

İçindekiler

• Frustum'un tanımı
  • Kesik piramidin özellikleri:
• Kesik piramidin alanını hesaplama formülü
  • Kesik piramidin yüzey alanı 
  • Kesik bir piramidin toplam yüzey alanı
• Kesik piramidin hacmini hesaplama formülü

Frustum'un tanımı

Kesik piramit, bir çokgenin tabanı ile tabanına paralel bir düzlemin kestiği kesit arasında kalan parçasıdır.

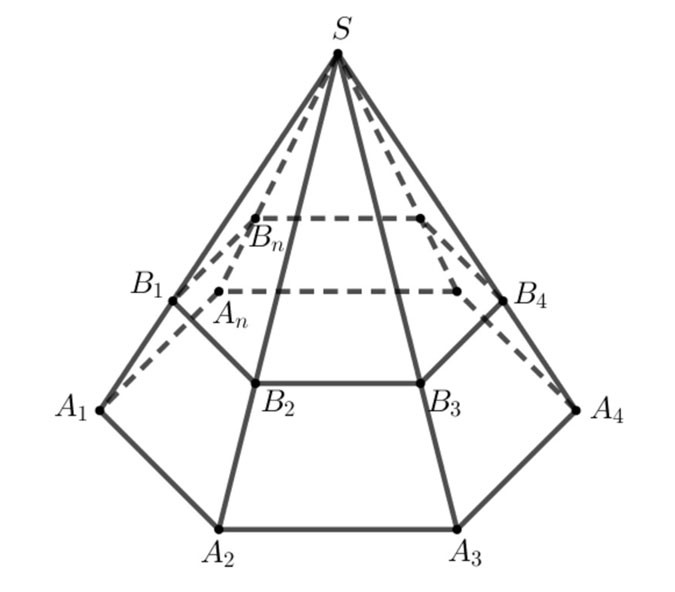
• A1A2...An,B1B2...BnA1A2...An,B1B2...Bn çokgenleri ve A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn yamuklarından oluşan şekle kesik piramit denir ve A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn şeklinde gösterilir.
• Basitçe ifade etmek gerekirse, S.A1A2...AnS.A1A2...An piramidi, S.B1B2...Bn.S.B1B2...Bn piramidi kesildikten sonra kesik bir piramit oluşturulur.

+ A1A2...An,B1B2...BnA1A2...An,B1B2...Bn çokgenlerine iki taban denir,

+ A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn trapezlerine yanal yüzler denir.

+ A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn doğru parçalarına yan kenarlar, taban yüzeyinin kenarlarına taban kenarları denir.

+ İki taban arasındaki mesafeye kesik piramidin yüksekliği denir.

Kesik piramidin özellikleri:

• İki taban, karşılıklı kenarları paralel ve karşılıklı kenar oranları eşit olan iki çokgendir (üçgen, dörtgen, beşgen, vb.).
• Yan yüzlerin hepsi yamuktur.
• Yan kenarları içeren doğrular bir noktada (piramidin tepesinde) birleşecektir.
• Kesik piramit, tabanları düzgün çokgenlerden (eşit kenarlı) oluşan piramittir. Dolayısıyla bir kesik koninin yan yüzleri birbirine eşit yamuklardır.

Kesik piramidin alanını hesaplama formülü

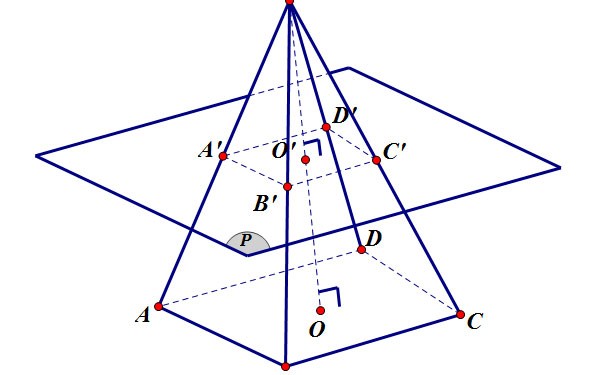
Kesik piramidin yüzey alanı

Kesik piramidin yanal alanı, kesik piramidi çevreleyen yüzlerin alanı, yani iki tabanın alanı hariç, kesik piramidi çevreleyen kısımdır.

Kesik piramidin yanal alanı nasıl hesaplanır: Kesik piramidin her bir yan yüzünün (yamukların) alanını, normal yamuk alanını hesaplama formülüne göre hesaplayın , ardından toplam alanı hesaplayın.

Düzgün kesik piramidin alanını hesaplama formülü:

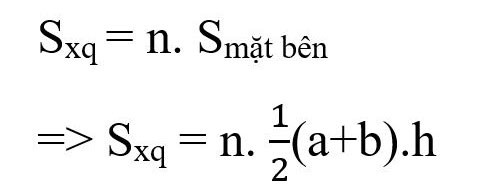
Orada:

• Sxq: çevre alanı
• n: kesik piramidin yanal yüzlerinin sayısı (taban çokgeninin kenar sayısına eşit)
• a, b: sırasıyla üst ve alt tabanların kenar uzunlukları
• h: dörtgenin kenar yüksekliği.

Örnek 1: 

Taban kenarları 10cm ve 15cm, kenar yüksekliği 12cm olan düzgün dörtgen kesik piramidin yan alanını hesaplayınız.

Ödül: 

Düzgün dörtgen kesik piramidin yan yüzü ikizkenar yamuk olduğundan bir yan yüzünün alanı kaçtır?

Düzgün dörtgen kesik piramidin 4 eşit kenarı vardır, dolayısıyla yan alanı:

150 x 4 = 600 (cm2)

Örnek 2: Taban kenarları 6cm ve 8cm, kenar yüksekliği 5cm olan düzgün dörtgen kesik piramidin yan alanını hesaplayınız. Taban kenarları 6cm ve 8cm olan düzgün dörtgen kesik piramidin yan alanını hesaplayınız.

Ödül: 

Düzenli dörtgen kesik piramidin yan yüzü ikizkenar yamuktur, bu nedenle bir yan yüzünün alanı eşittir

Düzenli bir dörtgen kesik piramidin dört eşit kenarı vardır, bu nedenle yan alanı eşittir

35 x 4 = 140 (cm2)

Kesik bir piramidin toplam yüzey alanı

Kesik piramidin toplam alanı, yanal alan ile iki taban alanının toplamına eşittir.

Formül:                    Stp = Sxq + Büyük dip + Küçük dip

Orada:

• Stp: Toplam alan
• Sxq: Çevre alanı
• Geniş taban: Geniş taban alanı
• Küçük taban: Küçük taban alanı

Örneğin: 

Şekilde verilen ölçülere göre düzgün kesik piramidin toplam alanını hesaplayınız.

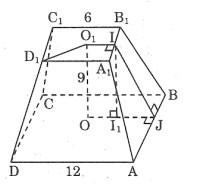
Ödül:

Sahibiz:

AD = 12 ⇒ OJ = 6

II1 ⊥ OJ çizin: I1J = 3

Pisagor teoremini II1J dik üçgenine uygularsak:

IJ2 = II12 + I1J2 = 92 + 32 = 90

Buradan:

Bir yamuk kenarının alanı:

Çevre alanı şuna eşittir:

Üst tabanın alanı: S = 6 x 6 = 36 (birim)

Alt taban alanı: S = 12 x 12 = 144 (birim)

Kesik bir piramidin toplam alanı şuna eşittir:

Kesik piramidin hacmini hesaplama formülü

Yemek tarifi:

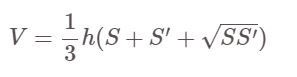
Orada:

• V: kesik piramidin hacmi
• S, S' sırasıyla piramidin büyük ve küçük taban alanlarını göstermektedir.
• h: piramidin yüksekliği, yani iki büyük ve küçük taban arasındaki mesafe

Kesik piramit bir kare midir (düzgün dörtgen):

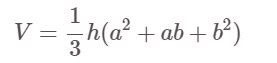
Orada:

• V: Hacim
• h: Piramidin yüksekliği
• a, b sırasıyla büyük tabanın ve küçük tabanın kenar uzunluklarıdır.