Düzenli, ikizkenar, eşkenar ve dik üçgenlerde yüksekliği hesaplama formülü

Üçgendeki yükseklik, önemli özelliklere sahip düz bir çizgidir ve düzlem geometri problemleriyle yakından ilişkilidir. Peki yükseklik nedir, üçgende yükseklik nasıl hesaplanır? Cevap ve üçgenin yüksekliğini hesaplamanın en basit formülü için lütfen aşağıdaki makaleye bakın.

İçindekiler

• Bir üçgende yüksekliği hesaplama formülü
  • Düzenli bir üçgende yüksekliği hesaplayın
  • Eşkenar üçgendeki yüksekliği hesaplayın
  • Dik üçgende yüksekliği hesaplama formülü
  • İkizkenar üçgende yüksekliği hesaplama formülü
• Bir üçgende yüksekliğin tanımı
• Bir üçgenin üç yüksekliğinin özellikleri

Bir üçgende yüksekliği hesaplama formülü

Düzenli bir üçgende yüksekliği hesaplayın

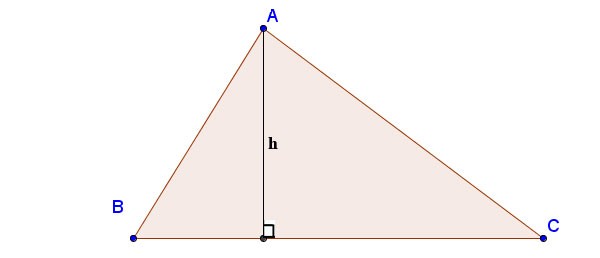
Heron formülü kullanılarak bir üçgenin yüksekliği nasıl hesaplanır:

a, b, c kenar uzunlukları olmak üzere; ha, A köşesinden BC kenarına çizilen yüksekliktir; p yarı çevredir:

Örneğin: 

ABC üçgeni verildiğinde, kenar AB = 4 cm, kenar BC = 7 cm, kenar AC = 5 cm'dir. A'nın BC'yi H noktasında kestiği noktadan itibaren AH yüksekliğini hesaplayıp, ABC'nin alanını hesaplayınız.

Ödül:

Üçgenin yarım çevresi: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Yükseklik   

=>

ABC üçgenini ele alalım:

Bu yüzden,

Eşkenar üçgendeki yüksekliği hesaplayın

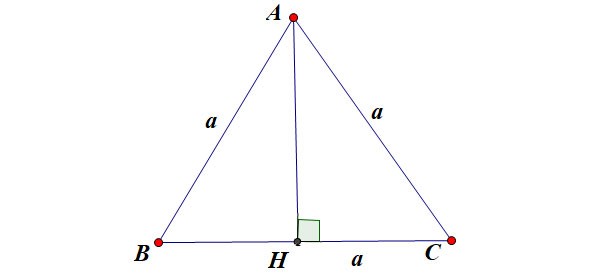
Eşkenar üçgen ABC'nin kenar uzunluğu şekilde gösterildiği gibi a olsun:

Orada:

• h eşkenar üçgenin yüksekliğidir
• a eşkenar üçgenin kenar uzunluğudur

Dik üçgende yüksekliği hesaplama formülü

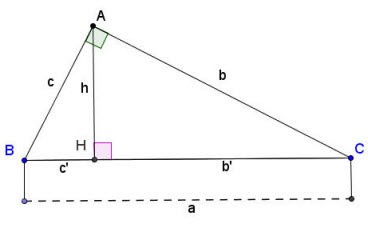
Yukarıda gösterildiği gibi A noktasında bir ABC dik üçgeni olduğunu varsayalım:

Dik üçgende kenar ve yükseklik hesaplama formülü:

1. a2 = b2 + c2

2. b2 = ab′ ve c2 = ac′

3.ah = bc

4. h2 = b′.c'

5.

Orada:

• a, b, c yukarıda gösterildiği gibi bir dik üçgenin kenarlarıdır;
• b', b kenarının hipotenüse izdüşümüdür;
• c', c kenarının hipotenüse izdüşümüdür;
• h, A dik açısının köşesinden BC hipotenüsüne kadar çizilen bir dik üçgenin yüksekliğidir.

Örnek 1: A noktasında dik açılı ABC üçgeni ve yüksekliği AH verilmiştir. AB = 15cm, HC = 16cm olduğunu bilerek BC, AC, AH'yi hesaplayınız.

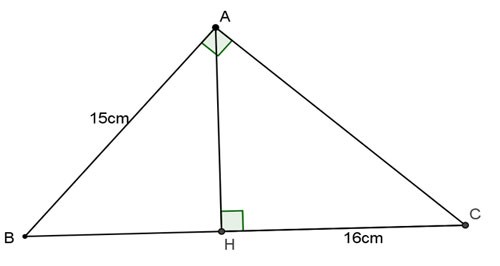
Ödül:

Cebirsel formülü ABC dik üçgenine uygularsak:

AC2 = CH.BC = 16.BC

A açısına sahip ABC dik üçgeni için Pisagor teoremine göre:

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (M.Ö. - 25)(M.Ö. + 9) = 0

⇔ BC = 25 veya BC = -9 (eleyin)

⇒ AC2 = 16.BC = 16.25 = 400 ⇒ AC = 20 (cm)

ABC dik üçgenini şu şekilde ele alalım: AH.BC = AB.AC (geometrik formül)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Yani BC=25(cm); AC=20(cm); AH=12(cm)

Örnek 2 :

Verilen ABC üçgeni A noktasına diktir, AB=24cm, AC=32cm. BC'nin dik açıortayı AC, BC'yi sırasıyla D ve E noktalarında keser. DE'yi hesaplayın.

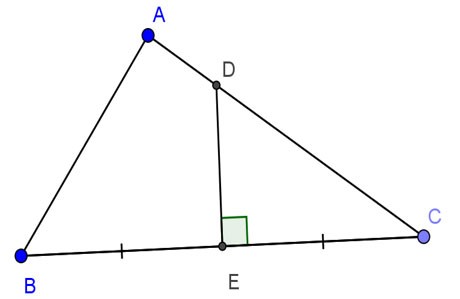
Ödül:

ABC dik üçgenini ele alalım:

BC2 = AB2 + AC2 (Pisagor teoremine göre)

BC2 = 242 + 322

BC2 = 1600

MÖ = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Dik üçgen ACB ve dik üçgen ECD'yi ele alalım:

∠A = ∠E = 90o var

∠C ortak

=> Üçgen ACB ∾ üçgen ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Yani ED = 15cm

İkizkenar üçgende yüksekliği hesaplama formülü

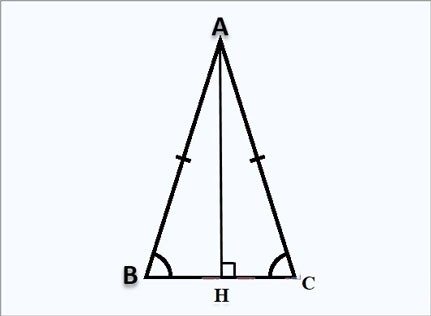
Diyelim ki A noktasında ABC ikizkenar üçgeniniz var, AH yüksekliği yukarıda gösterildiği gibi H noktasına diktir:

AH yüksekliğini hesaplama formülü:

ABC üçgeni A noktasında ikizkenar olduğundan, AH yüksekliği aynı zamanda kenarortaydır, dolayısıyla:

⇒ HB=HC= ½BC

Pisagor teoremini H noktasındaki ABH dik üçgenine uygularsak şunu elde ederiz:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Örnek : Δ ABC, BC = 30(cm), yükseklik AH = 20(cm) olacak şekilde A noktasında dengededir. Bu ikizkenar üçgenin kenarına denk gelen yüksekliği hesaplayınız.

Çözüm: Δ ABC'nin A noktasında ikizkenar olduğunu ve BC = 30(cm) olduğunu düşünün

⇒ BH = CH = 15(cm).

Pisagor teoremini uygularsak:

Şimdi BK = ? hesaplamamız gerekiyor.

Sahibiz:

Diğer taraftan

Bu nedenle, ⇔

Bir üçgende yüksekliğin tanımı

Bir üçgende yükseklik, bir köşeden karşı kenara çizilen dik doğru parçasıdır. Bu karşı tarafa yüksekliğe karşılık gelen taban denir. Yüksekliğin uzunluğu, en üst nokta ile en alt nokta arasındaki mesafedir.

Bir üçgenin üç yüksekliğinin özellikleri

Bir üçgenin üç yüksekliği aynı noktadan geçer. İşte bu noktaya üçgenin diklik merkezi denir .

Bir üçgenin yüksekliğini hesaplayabilmek için yukarıdaki formüllerde bilinmeyen bileşenleri hesaplamanız yeterlidir.

• Odak noktası nedir? Bir üçgenin ağırlık merkezini hesaplama formülü