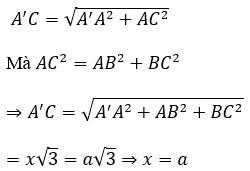Prizma, iki paralel ve eşit tabandan ve paralelkenar yan yüzeylerinden oluşan çokgendir.
Yorum:
Bir prizmanın (V prizması) hacmini hesaplama formülü nedir ve dikey prizmanın hacmini hesaplama formülü nedir? Lütfen aşağıdaki makaleye bakınız.
İçindekiler
Dikey prizmanın hacmini hesaplama formülü:
Dik prizmanın hacmi, taban alanı ile yüksekliğin çarpımına eşittir.
Orada
Vprizmanın hacmi (birim m3)Btaban alanıdır (birim m2)hprizmanın yüksekliğidir (birim m)Düzgün çokgen tabanlı dikey bir prizmadır. Prizmanın yan yüzleri birbirine eşit dikdörtgenlerdir. Mesela: düzgün üçgen prizma, düzgün dörtgen... o zaman bunu düzgün prizma olarak anlarız.
Düzgün dörtgen tabanına düzgün dörtgen prizması denir.
Üçgen prizma
Örneğin:
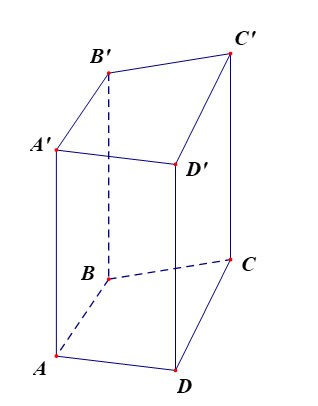
ABC.A'B'C' üçgen prizması şu şekildedir:
- Alt taban ABC üçgeni, üst taban A'B'C' üçgenidir;
Yan yüzler dikdörtgendir: AA'B'B, BB'C'C, CC'A'A;
- Kenarlar:
- Köşeler: A, B, C, A', B', C'.
- Yükseklik bir kenarın uzunluğudur: AA' veya BB' veya CC'.
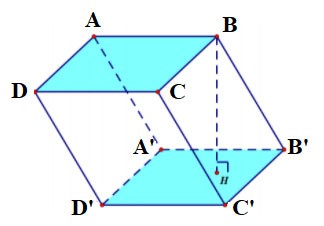
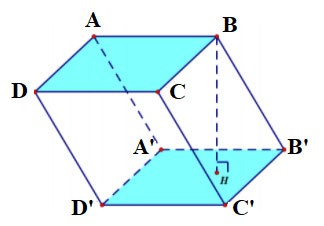
Dörtgen prizma
- Dörtgen prizmanın 6 yüzü, 12 kenarı ve 8 köşesi vardır.
- Her iki taban da dörtgen olup birbirine paraleldir. Her bir yan yüz bir dikdörtgendir.
- Kenarları eşittir.
- Dörtgen prizmanın yüksekliği bir kenarının uzunluğuna eşittir.
Örneğin:
Dörtgen prizma ABCD.A'B'C'D' şu şekildedir:
- Alt taban ABCD dörtgeni, üst taban A'B'C'D' dörtgenidir;
Yan yüzler dikdörtgendir: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Kenarlar:
+ Taban kenarları: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Yan kenarlar: AA', BB', CC', DD' eşittir.
- Köşeler: A, B, C, D, A', B', C', D'.
- Yükseklik bir kenarın uzunluğudur: AA' veya BB' veya CC' veya DD'.
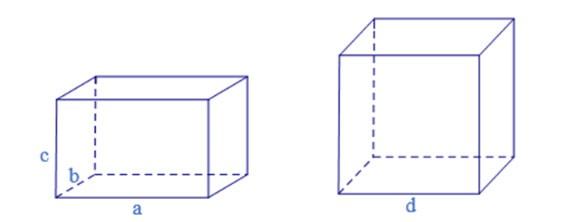
Not: Dikdörtgen prizmalar ve küpler de aynı zamanda dörtgen prizmalardır.
Bir prizmanın yan kenarları tabanına dik ise buna dik prizma denir.
Not:
Tabanı dikdörtgen olan dörtgenin düşey silindirine dikdörtgen kutu denir.
Eğer bir dörtgen silindirin 12 kenarı a uzunluğunda ise o zaman ona küp denir.
Sağ prizma ile normal prizmayı karşılaştırın:
| TANIMLAMAK: | DOĞA |
| + Dikey prizma, tabanına dik bir kenarı olan prizmadır. |
+ Düşey prizmanın yan yüzleri dikdörtgendir. + Prizmanın yan yüzleri taban yüzüne diktir. + Yükseklik yandır |
| + Düzgün prizma, tabanı düzgün çokgen olan düşey prizmadır. |
+ Prizmanın yan yüzleri birbirine eşit dikdörtgenlerdir. + Yükseklik yandır |
Örnek 1:
Tabanı ABC olan ve kenarı a = 2 cm ve yüksekliği h = 3 cm olan eşkenar üçgenin ABC.A'B'C' prizması verilmiştir. Bu prizmanın hacmini hesaplayınız?
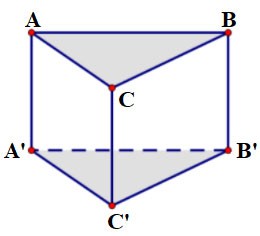
Ödül:
Tabanı bir kenarı a olan eşkenar üçgen olduğundan alanı:
Bu anda prizmanın hacmi:
Örnek 2:
Alıştırma 1: Kenarları AB = 3a, AD = 2a, AA'= 2a olan dikey bir kutu verilmiştir. A'.ACD' bloğunun hacmini hesaplayın
Talimat:
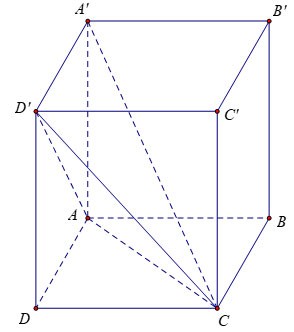
ADD'A' yan yüzü bir dikdörtgen olduğundan:
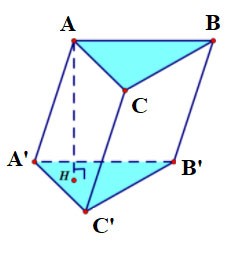
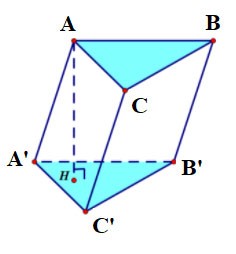
Örnek 3 : Tabanı bir kenarı a√3 olan eşkenar üçgen olan ABC.A'B'C' dikey prizması verildiğinde, taban ile prizma arasındaki açı 60º'dir. BB'nin orta noktası M olsun. M.A'B'C' piramidinin hacmini hesaplayınız.
Ödül:
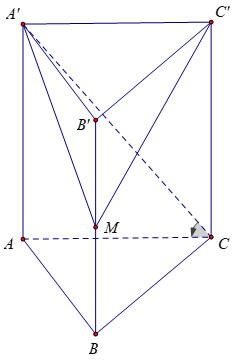
Bu nedenle şunu çıkarabiliriz ki
Sahibiz:
Örnek 4:
Taban kenarı uzunluğu a ve yüzü (DBC') olan ve tabanı ABCD ile 60º açı yapan düzgün bir dörtgen prizma ABCD.A'B'C'D' verilmiştir. ABCD.A'B'C'D prizmasının hacmini hesaplayınız?
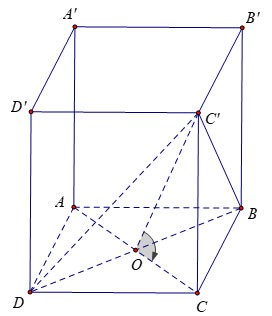
ABCD karesinin merkezinde O noktası var.
Öte yandan bu nedenle
Çıkarım yapmak
Ayrıca:
Örnek 5:
ABCD.A'B'C'D' küpünün hacmini hesaplayın, AC'=a√3 olduğunu bilerek
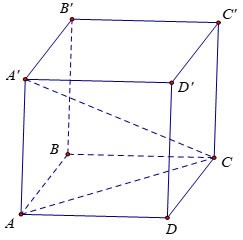
Ödül:
Küpün kenar uzunluğu x olsun.
A noktasına dik açılı AA'C üçgenini ele alalım:
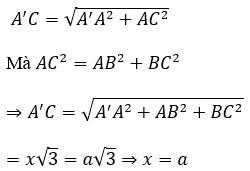
Dolayısıyla küpün hacmi V=a^3'tür.
Yukarıdaki prizmanın hacmini hesaplama formülüne ek olarak, dönel bir cismin hacmini hesaplama formülü , bir dairenin alanı ve çevresini hesaplama formülü ile ilgili diğer makalelere de başvurabilirsiniz ...
Microsoft Teams'te "Lisans Hatası" ile mi karşılaşıyorsunuz? Lisans sorunlarını hızlıca çözmek, erişimi geri yüklemek ve BT ekibiyle uğraşmadan verimliliği artırmak için bu adım adım sorun giderme kılavuzunu izleyin. En son düzeltmelerle güncellendi.
Microsoft Teams Ücretsiz Abonelik Hatası yüzünden toplantılarınızın aksamasından bıktınız mı? Sorunu hızlıca çözmek ve sorunsuz ekip çalışmasını yeniden sağlamak için kanıtlanmış, adım adım çözümleri keşfedin. En yeni sürümlerde çalışır!
Herkese açık Wi-Fi ağlarında Microsoft Teams ağ hatasıyla mı karşılaşıyorsunuz? Aramalarınızı ve toplantılarınızı sorunsuz bir şekilde geri yüklemek için VPN ayarları, port kontrolleri ve önbellek temizleme gibi anında çözümler bulun. Hızlı çözüm için adım adım kılavuz.
Microsoft Teams Wiki sekmesinin yüklenmemesi hatasıyla mı karşılaşıyorsunuz? Sorunu hızlıca çözmek, Wiki sekmelerinizi geri yüklemek ve ekip verimliliğini sorunsuz bir şekilde artırmak için kanıtlanmış adım adım çözümleri keşfedin.
Microsoft Teams Mac'te Anahtar Zinciri hatasıyla mı mücadele ediyorsunuz? Sorunsuz iş birliğine geri dönmek için macOS için kanıtlanmış, adım adım sorun giderme çözümlerini keşfedin. Hızlı çözümler içeride!
Microsoft Teams mikrofonunuzda boğuk veya hiç ses olmamasından bıktınız mı? Microsoft Teams mikrofon sorunlarını hızlı ve kanıtlanmış adımlarla nasıl çözeceğinizi keşfedin. Net ses sizi bekliyor!
Microsoft Teams QR kodunun nerede olduğunu ve mobil cihazınızdan süper hızlı nasıl giriş yapabileceğinizi tam olarak keşfedin. Adım adım, görsellerle desteklenmiş kılavuz sayesinde saniyeler içinde bağlantı kurabilirsiniz—şifreye gerek yok!
Microsoft Teams'in yavaş çalışmasından mı rahatsızsınız? Microsoft Teams'in neden bu kadar yavaş olduğunu keşfedin ve 2026'da sorunsuz bir iş birliği için hızını önemli ölçüde artırmak üzere bu 10 kanıtlanmış ipucunu uygulayın.
Bilgisayarınızda Microsoft Teams kurulum klasörünü bulmakta zorlanıyor musunuz? Bu adım adım kılavuz, yeni ve klasik Teams sürümleri için, kullanıcı ve makine bazında kurulumların tam yollarını gösteriyor. Sorun gidermede zamandan tasarruf edin!
Microsoft Teams Görev Yönetimi Senkronizasyon Hatalarının iş akışınızı aksatmasından bıktınız mı? Teams, Planner ve To Do genelinde sorunsuz görev senkronizasyonunu geri yüklemek için uzmanlarımızın adım adım çözümlerini izleyin. Anında rahatlama için hızlı çözümler!
Microsoft Teams Copilot'ı kullanarak yapay zeka destekli verimliliği nasıl artıracağınızı keşfedin. Toplantıları, sohbetleri ve görevleri zahmetsizce dönüştürmek için adım adım kılavuz, temel özellikler ve ipuçları. Daha akıllı iş birliğinin kilidini bugün açın!
Microsoft Teams'in yavaş çalışmasından mı şikayetçisiniz? Windows, Mac, web ve mobil cihazlarda performans sorunlarını, gecikmeleri, çökmeleri gidermek ve hızı artırmak için Microsoft Teams önbelleğini adım adım nasıl temizleyeceğinizi öğrenin. İşe yarayan hızlı çözümler!
"Teams Takvimim Nerede?" sorunuyla mı boğuşuyorsunuz? Microsoft Teams'deki senkronizasyon sorunlarını adım adım çözün. Takvim görünümünüzü geri yükleyin ve zahmetsizce senkronize edin—uzman ipuçları içeride!
Chromebook'larda Microsoft Teams oturum açma hatasıyla mı karşılaşıyorsunuz? Oturum açma sorunlarını hızlıca çözmek için adım adım çözümleri keşfedin. Sorunsuz ekip çalışması için önbelleği temizleyin, uygulamaları güncelleyin ve daha fazlasını yapın. En yeni Chrome OS sürümlerinde çalışır!
Microsoft Teams'te küçük yazı tipleriyle mi mücadele ediyorsunuz? Microsoft Teams arayüzünüzü daha büyük ve daha okunaklı hale getirmek için kanıtlanmış adımları keşfedin. Masaüstü, web ve erişilebilirlik ayarları için kolay düzenlemelerle netliği artırın ve göz yorgunluğunu azaltın.
