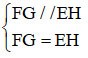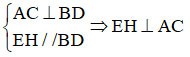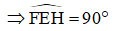Karenin köşegeni nasıl hesaplanır, dikdörtgenin köşegeni nasıl hesaplanır konuları matematik problemlerinde ve tasarım ve inşaat, köşe kesme, ölçme gibi pratik uygulamalarda çokça kullanılmaktadır. Quantrimang.com iki köşegenin özellikleri hakkında bilgi ve hesaplama formüllerini derlemiştir, lütfen çalışmanızda, hayatınızda ve işinizde uygulayabilmeniz için başvurunuz.
İçindekiler
Kare ve dikdörtgenin köşegeni kaçtır?
Kare veya dikdörtgenin köşegeni , karşılıklı iki köşeyi birleştiren çizgidir. Her kare ve dikdörtgenin eşit uzunlukta iki köşegeni vardır.
Bir karenin köşegeni nasıl hesaplanır
Kare köşegenin özellikleri
- Karenin iki köşegeni eşit uzunluktadır, birbirine diktir ve köşegenlerin orta noktasında kesişirler.
- Bir iç teğet çember ve bir dış teğet çember vardır ve her iki çemberin merkezleri çakışmakta olup, karenin iki köşegeninin kesişim noktalarıdır.
- 1 köşegen, kareyi iki dik ikizkenar üçgene bölecektir.
- Açıortayların, kenarortayların ve dik ortayların kesişim noktaları aynı noktada çakışır.
- Dikdörtgen, paralelkenar ve eşkenar dörtgenin tüm özelliklerini taşır.
Bir karenin köşegenini hesaplama formülü
Karenin özelliklerine göre, karenin iki köşegeni birbirine eşittir ve bir köşegeni kareyi iki eşit alana böler, bu parçalar iki ikizkenar dik üçgendir. Dolayısıyla karenin köşegeni iki ikizkenar dik üçgenin hipotenüsüdür.
Yani bir karenin köşegenini hesaplamak için Pisagor teoremini dik üçgene uygulamak yeterlidir.
Kenar uzunluğu a olan ABCD karesini varsayalım; AC köşegeni kareyi ABC ve ACD olmak üzere iki dik üçgene böler.
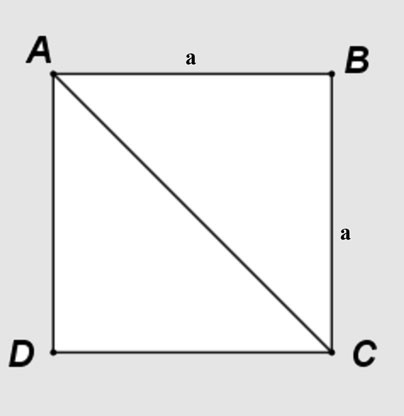
Pisagor teoremini ABC dik ikizkenar üçgenine uygulayalım:
⇒ ⇒
Yani bir karenin köşegeninin kenar uzunluğu a'dır:
Bir karenin köşegeninin hesaplanmasına örnek
Örnek 1: Bir karenin kenarı 3cm'dir. Bu karenin köşegeni nedir: 6cm, √18cm, 5cm veya 4cm?
Çözüm:
a) ABC karesinde Pisagor teoremini uygularsak:
AC² = AB² + BC² = 3² + 3² = 18
=> AC = cm
Yani karenin köşegeni √18 cm'dir.
Örnek 2:
Bir karenin köşegeni 2dm'dir. Bu karenin kenarı kaçtır: 1cm, 3/2cm, √2cm veya 4/3cm?
Ödül:
Pisagor teoremini ABC dik üçgenine uygulayın, ancak bu alıştırmada köşegenin uzunluğu yani AC = 2cm veriliyor, AB kenarını hesaplayın.
Şunu elde ederiz: AC² = AB² + BC² = 2AB (çünkü AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Bir dikdörtgenin köşegeni nasıl hesaplanır
Dikdörtgen, dört dik açısı olan dışbükey dörtgen, iki eşit köşegeni olan paralelkenardır.
Bir dikdörtgenin köşegenlerinin özellikleri
Bir dikdörtgenin köşegenleri, dikdörtgenler ve köşegenleriyle ilgili problemleri çözmede yararlı olan birkaç önemli özelliğe sahiptir.
- Bir dikdörtgenin köşegeninin uzunluğu, dik üçgenin hipotenüsüne eşittir, yani iki kenarın kareleri toplamının kareköküne eşittir.
- Köşegen dikdörtgeni alanları eşit iki dik üçgene böler. Yani bir dikdörtgenin köşegeni, dikdörtgenin simetri eksenidir.
- Bir dikdörtgenin iki köşegeni birbirine eşittir ve her doğrunun orta noktasında kesişerek 4 tane ikizkenar üçgen oluşturur.
Bir dikdörtgenin köşegenini hesaplama formülü
Yukarıdaki dikdörtgenin köşegeninin özelliklerinden yola çıkarak Pisagor teoremini kullanarak dikdörtgenin köşegeninin uzunluğunu hesaplayabiliriz.
Aşağıda gösterildiği gibi uzunluğu a, genişliği b, köşegeni AC olan bir ABCD dikdörtgeniniz olduğunu varsayalım.
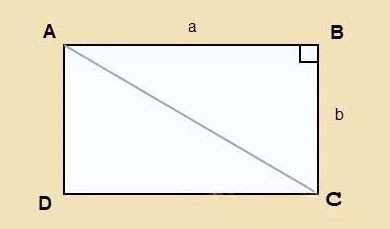
Pisagor teoremini ABC dik üçgenine uygulayalım:
⇒ ⇒
Dolayısıyla, uzunluğu a ve genişliği b olan bir dikdörtgenin köşegeni:
Yani bir dikdörtgenin köşegeninin uzunluğu, dikdörtgenin iki kenarının (uzunluk ve genişlik) karelerinin toplamının kareköküne eşittir.
Dolayısıyla bir karenin veya dikdörtgenin köşegenini Pisagor teoremini uygulayarak kolayca hesaplayabiliriz.
Dikdörtgenin köşegeninin hesaplanmasına örnek
Uzunluğu 10dm ve genişliği 5dm olan bir dikdörtgenin köşegen uzunluğunu hesaplayınız.
Çözüm:
Dikdörtgenin köşegeninin uzunluğu a olsun (a > 0, dm)
Pisagor teoremini uygulayarak dikdörtgenin köşegeninin uzunluğu:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Bir dörtgenin dikdörtgen olduğunu ispatlayan örnek.
Bir dikdörtgenin köşegeninin hesaplanması için kullanılan özellikler ve formül, bir dörtgenin dikdörtgen olduğunu kanıtlayan bazı problemleri çözmek için kullanılabilir.
Verilen ABCD dörtgeninin birbirine dik iki köşegeni vardır. AB, BC, CD, AD kenarlarının orta noktaları sırasıyla E, F, G, H olsun. EFGH dörtgeni nasıl bir şekildir? Neden?
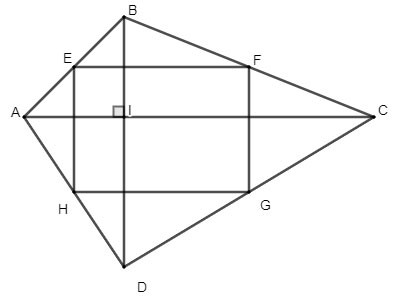
Çözüm:
Çünkü E, AB'nin orta noktasıdır, H ise AD'nin orta noktasıdır
=> EH, ABD üçgeninin medyanıdır.
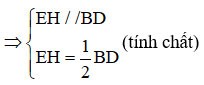 (1)
(1)
Çünkü F, BC'nin orta noktasıdır, G ise CD'nin orta noktasıdır
=> FG, BCD üçgeninin medyanıdır
 (2)
(2)
(1) ve (2)'den =>
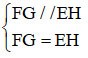
EFGH dörtgenini ele alalım.
FG // EH
FG = EH
=> EFGH bir paralelkenardır (tanıma işareti)
Diğer taraftan:
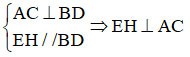
Ayrıca şunlar da var:
E, AB'nin orta noktasıdır, F ise BC'nin orta noktasıdır.
=> EF, ABC üçgeninin medyanıdır
=> EF // AC
Ama EH ⊥ AC => EH ⊥ EF
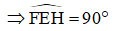
EFGH paralelkenarının dik açısı vardır
=> EFGH bir dikdörtgendir




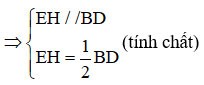 (1)
(1) (2)
(2)