Bir eşkenar dörtgenin köşegenini hesaplama formülü

Eşkenar dörtgen, dört kenarı birbirine eşit olan dörtgen, iki köşegeni orta noktasında birbirine dik olan dörtgen eşkenar dörtgen, iki komşu kenarı eşit olan paralelkenar... Kare, dikdörtgen, üçgen gibi şekillerin yanı sıra eşkenar dörtgen, matematikte ve yaşamda önemli şekillerden biridir.

Eşkenar dörtgenin çevresini ve alanını hesaplama formülünün yanı sıra , eşkenar dörtgenin köşegenini, yani eşkenar dörtgenin zıt köşelerini birbirine bağlayan doğruyu hesaplama yöntemi de çok önemlidir.

Aşağıdaki makale, bir eşkenar dörtgenin köşegeninin nasıl hesaplanacağını özel örneklerle öğrenmenize yardımcı olacaktır, lütfen bu makaleye bakın.

İçindekiler

• Bir eşkenar dörtgenin köşegeni
• Bir eşkenar dörtgenin köşegenlerinin özellikleri
• Bir eşkenar dörtgenin köşegenini hesaplama formülü
• Eşkenar dörtgenin köşegeninin hesaplanması problemi

Bir eşkenar dörtgenin köşegeni

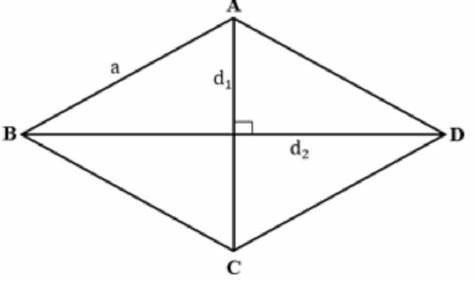
• Bir eşkenar dörtgenin köşegeni, eşkenar dörtgenin zıt iki köşesini birleştiren çizgidir.
• Bir eşkenar dörtgenin iki köşegeni vardır ve bunlar eşkenar dörtgenin orta noktasında kesişirler.
• Köşegen eşkenar dörtgeni eşit kenarlı iki eşkenar üçgene böler.

Bir eşkenar dörtgenin köşegenlerinin özellikleri

Bir eşkenar dörtgenin iki köşegeni aşağıdaki özelliklere sahiptir:

• İki eşit köşegen: Bir eşkenar dörtgenin iki köşegeni eşit uzunluktadır.
• İki köşegen arasındaki açı dik açıdır: Bir eşkenar dörtgenin iki köşegeni eşkenar dörtgenin orta noktasında kesişir ve dik açı oluşturur.
• Köşegenler eşkenar dörtgenin simetri eksenleridir: Eşkenar dörtgenin her köşegeni eşkenar dörtgenin simetri ekseni olup eşkenar dörtgeni iki simetrik yarıya böler.
• Köşegenler, iki eşkenar üçgenin köşegenleridir: Bir eşkenar dörtgenin her köşegeni, eşit kenarlardan oluşan iki eşkenar üçgenin köşegenidir.
• İki köşegenin uzunluklarının çarpımı, bir eşkenar dörtgenin iki kenarının uzunluklarının çarpımına eşittir: İki köşegenin uzunluklarının çarpımı, bir eşkenar dörtgenin iki kenarının uzunluklarının çarpımına eşittir. Yani köşegeni d, kenarları a ve b ile gösterirsek d² = a² + b² elde ederiz.

Bu özellikler eşkenar dörtgenlerin karakteristik özellikleridir ve eşkenar dörtgenlerle ilgili birçok geometrik problemde kullanılır.

Bir eşkenar dörtgenin köşegenini hesaplama formülü

Bir eşkenar dörtgenin köşegenini hesaplama formülünü elde etmek için lütfen aşağıdaki örneği inceleyin.

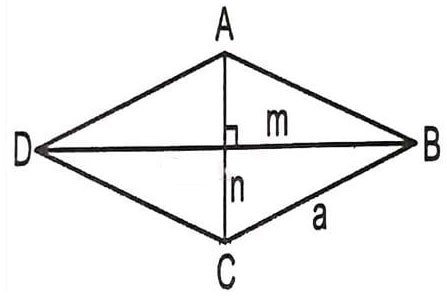
Kenarı a ve açısı ABC = 60 derece olan ABCD eşkenar dörtgeninin köşegeninin uzunluğunu hesaplamamız gerektiğini varsayalım -> bu durumda eşkenar dörtgenin köşegenini hesaplama formülü nedir?

Çözüm:

ABCD bir eşkenar dörtgen olduğundan tüm kenarları a'ya eşittir.

ABC üçgenini şu şekilde ele alalım: AB = BC = a

Tekrar: ABC = 60 derece => ABC üçgeni, kenarı a olan bir eşkenar üçgendir.

=> AB = AC = BC = a

=> Eşkenar dörtgenin köşegeninin uzunluğu AC = BD = a'dır.

Yukarıdaki çözüm bir eşkenar dörtgenin köşegenini hesaplamak için en basit ve anlaşılması en kolay formüllerden biridir.

Alan ve kalan köşegen bilindiğinde bir eşkenar dörtgenin köşegenini hesaplama formülü

Bir eşkenar dörtgenin alanını hesaplama formülünden:

S = (axb) : 2

Köşegen uzunluğu formülümüz şu şekildedir:

a = S x 2 : b

veya

b = S x 2 : a

Orada:

• S alanıdır
• a ve b iki köşegenin uzunluklarıdır

Pisagor teoremini kullanmadan eşkenar dörtgenin geometrik özelliklerini kullanarak köşegeninin uzunluğunu hesaplayın. Özellikle:

Bir eşkenar dörtgenin köşegeni iki yüksekliğin ortalamasıdır.

Köşegen = (uzun yükseklik + kısa yükseklik)²'nin karekökü

Bir eşkenar dörtgenin köşegeni, eşkenar dörtgenin çevresinin yarısıdır.

Köşegen = 1/2 x eşkenar dörtgenin çevresi.

Eşkenar dörtgenin köşegeninin hesaplanması problemi

Soru 1: Alanı 360 santimetrekare, köşegen uzunluğu 24 santimetre olan bir eşkenar dörtgen verilmiştir. İkinci köşegenin uzunluğunu hesaplayın

Çözüm:

Bir eşkenar dörtgenin alan formülüne göre: axb : 2

İkinci köşegenimiz: 360 x 2 : 24 = 30cm

Cevap: 30cm

Sorun 2:

Bir eşkenar dörtgenin alanı 4dm, bir köşegeninin uzunluğu ise 3/5 dm'dir. İkinci köşegenin uzunluğunu hesaplayınız. Çözüm:

İkinci köşegenin uzunluğu:

(4 x 2) : 3/5 =40/3 (dk)

Ders 3: Bir eşkenar dörtgenin iki köşegeninin uzunlukları 160 cm ve 120 cm'dir. Eşkenar dörtgenin kenar uzunluğu ile yüksekliği arasındaki oranın 24:25 olduğunu bilerek eşkenar dörtgenin yüksekliğini hesaplayınız.

Çözüm:

Eşkenar dörtgenin alanı: 160.120:2 = 9 600 (cm2) dir.

Bir eşkenar dörtgenin yüksekliği ile bir kenar uzunluğu arasındaki oran 24:25 olduğundan, eşkenar dörtgenin yüksekliğini 24a, bir kenarını da 25a olarak kabul edebiliriz.

O zaman eşkenar dörtgenin alanı şu şekilde olur: 25a.24a = 9 600 a2 = 16 a = 4 cm

Eşkenar dörtgenin yüksekliği: 24,4 = 96 (cm) dir.

Yani eşkenar dörtgenin yüksekliği 96 cm'dir.

Ders 4: 

Kenar uzunluğu 12,5 cm, yüksekliği 6,72 cm olan ve AC'nin BD'den küçük olduğu ABCD eşkenar dörtgeni verilmiştir. AC ve BD köşegenlerinin uzunlukları sırasıyla kaçtır?

Ödül:

Eşkenar dörtgenin alanını hesaplamak için formülü uygulayın: S = ha = 6,72 x 12,5 = 84cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Bir eşkenar dörtgenin iki köşegeninin kesişim noktası O olsun.

AOB'nin O noktasında dik üçgen olduğunu varsayalım, dolayısıyla AB2 = OA2 + OB2

Burada, OA = 1/2 AC, OB = 1/2 BD

=> 12.52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2 + 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (Probleme göre BD > AC) (2)

(1) ve (2)'den şunu elde ederiz:

BD = 24, AC = 7cm.

Ders 5: 

ABCD eşkenar dörtgeninin kenarları 10 birime eşittir. Eşkenar dörtgenin köşegeninin uzunluğunu hesaplayınız.

Çözüm: ABCD eşkenar dörtgeninin köşegeninin uzunluğu:

Köşegen = 2'nin karekökü (10²) = 200'ün karekökü = 14,14 birim uzunluk.

O halde ABCD eşkenar dörtgeninin köşegeninin uzunluğu 14,14 birimdir.

Ders 6:

ABCD eşkenar dörtgeninin köşegeni 12 birimdir. Eşkenar dörtgenin çevresini hesaplayınız.

Çözüm: Bir eşkenar dörtgenin dört eşit kenarı olduğundan çevresi, dört kenarın uzunluklarının toplamına eşit olacaktır, yani:

Çevre = 4 x kenar uzunluğu = 4 x 6 = 24 birim uzunluk.

Yani ABCD eşkenar dörtgeninin çevresi 24 birim uzunluğundadır.