Normal TV ile Akıllı TV arasındaki fark
Akıllı televizyonlar gerçekten dünyayı kasıp kavurdu. Teknolojinin sunduğu pek çok harika özellik ve internet bağlantısı, televizyon izleme şeklimizi değiştirdi.
10 tabanından 16 tabanına dönüştürme
Ondalık sistem (taban 10)
Ondalık sayı sistemi günlük yaşamda en yaygın kullanılan ve standart olan sistemdir. Bu sayma sistemi 10 sayısını temel alır. Ondalık sistem 0'dan 9'a kadar olan rakamlardan oluşan 10 karakterden oluşur. Özellikle 0, 1, 2, 3, 4, 5, 6, 7, 8 ve 9.
Bilinen en eski sayı sistemlerinden biri olan ondalık sayı sistemi, birçok antik uygarlık tarafından kullanılmıştır. Çok büyük sayıların ondalık sistemde temsil edilmesindeki zorluk, Hint-Arap rakam sistemiyle aşıldı. Hint-Arap rakam sistemi bir sayıdaki rakamların yerlerini belirler. Her basamak 10'un bir kuvvetine eşittir ve ondalık noktadan önceki en sağ basamak olan 100'den başlar.
Örneğin, 2345.67 sayısının ondalık gösterimi:
- 5 rakamı birler basamağındadır (100=1),
- 4 rakamı onlar basamağındadır (101)
- 3 rakamı yüzler basamağındadır (102)
- 2 rakamı binler basamağındadır (103)
- Bu arada, virgülden sonraki 6 rakamı 1/10 (10-1) konumunda, 7 ise 1/100 (10-2) konumundadır.
Dolayısıyla 2345,67 sayısı şu şekilde de gösterilebilir: (2 * 103) + (3 * 102) + (4 * 101) + (6 * 10-1) + (7 * 10-2).
10 tabanındaki sayının 16 tabanına dönüştürülmesine örnek:
- (79)10 = (4F)16
- (120)10 = (78)16
- (1728)10 = (6C0)16
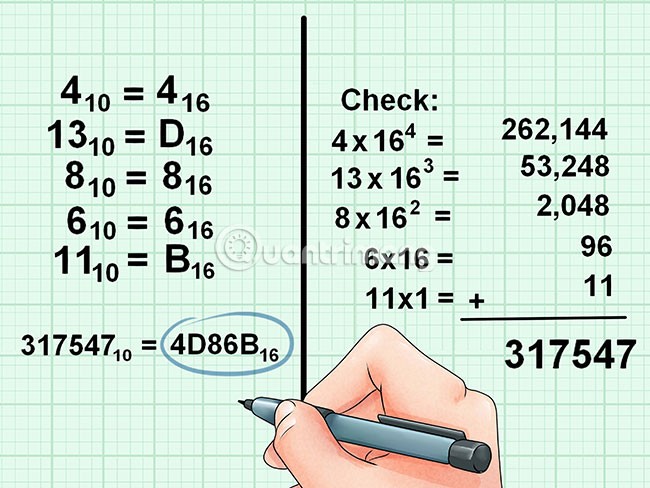
Onaltılık (taban 16)
Hexadecimal, Hex veya onaltılık sayı sistemi, 16 tabanlı bir sayı sistemi kullanır ve uzun ikili değerleri temsil etmek için popüler bir seçimdir, çünkü biçimleri yalnızca 1 ve 0 değerlerinden oluşan uzun ikili dizelere göre çok daha kompakt ve anlaşılması daha kolaydır.
Taban 10'dan Taban 16'ya Dönüşüm Tablosu
| 10'lu taban sistemi | Onaltılık sistem |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Ayrıca bakınız:
Dondurucuda ışık yokken buzdolabında neden ışık var?
Buzdolapları evlerde sıkça kullanılan cihazlardır. Buzdolapları genellikle 2 bölmeden oluşur, soğutucu bölme geniştir ve kullanıcı her açtığında otomatik olarak yanan bir ışığa sahiptir, dondurucu bölme ise dardır ve hiç ışığı yoktur.
Wi-Fiyi Yavaşlatan Ağ Tıkanıklığını Gidermenin 2 Yolu
Wi-Fi ağları, yönlendiriciler, bant genişliği ve parazitlerin yanı sıra birçok faktörden etkilenir; ancak ağınızı güçlendirmenin bazı akıllı yolları vardır.
Tenorshare Reiboot Kullanarak Veri Kaybı Olmadan iOS 17den iOS 16ya Nasıl Geri Dönülür
Telefonunuzda kararlı iOS 16'ya geri dönmek istiyorsanız, iOS 17'yi kaldırma ve iOS 17'den 16'ya geri dönme konusunda temel kılavuzu burada bulabilirsiniz.
Her gün yoğurt yediğinizde vücudunuzda neler olur?
Yoğurt harika bir besindir. Her gün yoğurt yemek faydalı mıdır? Her gün yoğurt yediğinizde vücudunuzda nasıl değişiklikler olur? Hadi birlikte öğrenelim!
Hangi pirinç türü sağlık açısından daha iyidir?
Bu yazıda en besleyici pirinç türleri ve seçtiğiniz pirincin sağlık yararlarından nasıl en iyi şekilde yararlanabileceğiniz ele alınıyor.
Sabahları zamanında nasıl uyanılır
Uyku düzeninizi ve uyku vakti rutininizi oluşturmak, çalar saatinizi değiştirmek ve beslenmenizi buna göre ayarlamak, daha iyi uyumanıza ve sabahları zamanında uyanmanıza yardımcı olabilecek önlemlerden birkaçıdır.
Rent Please! oynamak için ipuçları Yeni Başlayanlar İçin Ev Sahibi Simülasyonu
Kiralayın Lütfen! Landlord Sim, iOS ve Android'de oynanabilen bir simülasyon mobil oyunudur. Bir apartman kompleksinin ev sahibi olarak oynayacak ve dairenizin içini iyileştirme ve kiracılar için hazır hale getirme amacıyla bir daireyi kiralamaya başlayacaksınız.
En Son Banyo Kule Savunma Kodları ve Kodların Nasıl Girileceği
Bathroom Tower Defense Roblox oyun kodunu alın ve heyecan verici ödüller için kullanın. Daha yüksek hasara sahip kuleleri yükseltmenize veya kilidini açmanıza yardımcı olacaklar.
Transformatörlerin yapısı, sembolleri ve çalışma prensipleri
Transformatörlerin yapısını, sembollerini ve çalışma prensiplerini en doğru şekilde öğrenelim.
Yapay Zekanın Akıllı TVleri Daha İyi Hale Getirmesinin 4 Yolu
Daha iyi görüntü ve ses kalitesinden ses kontrolüne ve daha fazlasına kadar, bu yapay zeka destekli özellikler akıllı televizyonları çok daha iyi hale getiriyor!
ChatGPT neden DeepSeekten daha iyidir
Başlangıçta DeepSeek'e yönelik büyük umutlar vardı. ChatGPT'ye güçlü bir rakip olarak pazarlanan bir yapay zeka sohbet robotu olarak, akıllı sohbet yetenekleri ve deneyimleri vadediyor.
Fireflies.ai ile tanışın: Size Saatlerce Çalışma Kazandıran Ücretsiz AI Sekreteri
Önemli ayrıntıları not alırken gözden kaçırmak kolaydır ve sohbet ederken not almaya çalışmak dikkat dağıtıcı olabilir. Çözüm Fireflies.ai'dır.
Axolotl Minecraft nasıl yetiştirilir, Minecraft Salamander nasıl evcilleştirilir
Axolot Minecraft, oyuncuların su altında görev yaparken nasıl kullanacaklarını bilmeleri durumunda harika bir yardımcı olacaktır.
Sessiz Bir Yer: Önümüzdeki Yol PC Oyun Yapılandırması
A Quiet Place: The Road Ahead'in yapılandırması oldukça yüksek olarak derecelendirilmiştir, bu yüzden indirmeye karar vermeden önce yapılandırmayı göz önünde bulundurmanız gerekecektir.